
����Ŀ��һ�ο����У���λѧ������ѧ�������ɼ����±���ʾ��

��1��Ҫ��5��ѧ����ѡ2�˲μ�һ������ѡ�е�ѧ����������һ�˵������ɼ�����90�ֵĸ��ʣ�

��2�������ϱ����ݣ�����ɢ��ͼ����ɢ��ͼ˵�������ɼ�![]() ����ѧ�ɼ�
����ѧ�ɼ�![]() ֮��������ع�ϵ��ǿ����������н�ǿ��������ع�ϵ����
֮��������ع�ϵ��ǿ����������н�ǿ��������ع�ϵ����![]() ��
��![]() �����Իع鷽�̣�ϵ����ȷ��0.01�������������������ع�ϵ����˵������.
�����Իع鷽�̣�ϵ����ȷ��0.01�������������������ع�ϵ����˵������.
�ο���ʽ��
�ع�ֱ�ߵķ�����![]() ������
������ ��
�� ![]() ��
��
![]() ����
����![]() ��Ӧ�Ļع����ֵ��
��Ӧ�Ļع����ֵ��
�ο����ݣ� ![]() ��
�� ![]() .
.
���𰸡�(1) ![]() ��(2)�𰸼�����.
��(2)�𰸼�����.
�����������������
(1)�������г����п��ܵ��¼�����Ϲŵ���ͼ��㹫ʽ�ɵ�������һ�˵������ɼ�����90�ֵĸ���Ϊ![]() ��
��
(2)����ɢ��ͼ���۲�ɵ������ɼ�����ѧ�ɼ��߶������.������Իع鷽�̵ļ��㹫ʽ�ɵã����Իع鷽��Ϊ![]() .
.
���������
(1)��5��ѧ������ȡ2��ѧ�����������Ϊ��(A1��A2)��(A1��A3)��(A1��A4)��(A1��A5)��(A2��A3)��(A2��A4)��(A2��A5)��(A3��A4)��(A3��A5)��(A4��A5)����10�����.
����������һ�˵������ɼ�����90�ֵ�����У�
(A1��A2)��(A1��A4)��(A2��A3)��(A2��A4)��(A2��A5)��(A3��A4)��(A4��A5)��7�������
��ѡ�е�ѧ����������һ�˵������ɼ�����90�ֵĸ���Ϊ![]() .
.
(2)
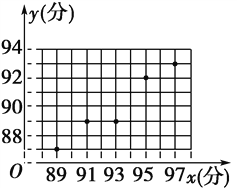
���Կ����������ɼ�����ѧ�ɼ��߶������.ɢ��ͼ��ͼ��ʾ��
��ɢ��ͼ���Կ�����Щ����·ֲ���һ��ֱ�߸��������������������������ɼ�����ѧ�ɼ������.
��y��x�����Իع鷽����![]() ��
��![]() x��
x��![]() ���������������ݣ����Լ����
���������������ݣ����Լ����
![]() ��93��
��93��![]() ��90,
��90,
![]() ��
��![]() ��0.75��
��0.75��![]() ��90��0.75��93��20.25��
��90��0.75��93��20.25��
����y��x�����Իع鷽����
![]() ��0.75x��20.25.
��0.75x��20.25.


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Ϊӭ��У�죬��У����ֱ��������ABC�ڵĿյ���ֲ��һ�顰�̵ء�ABD�����滮�ڡ�ABD���ڽ�������BEFG���ֻ�������ط��ֲݣ���AB=a����DAB=�ȣ��ֲݵ����ΪS1 �� �ֻ������ΪS2 �� ��ֵ ![]() ��Ϊ���滮��г�ȡ���
��Ϊ���滮��г�ȡ���
��1������a���ȱ�ʾS1 �� S2��
��2����aΪ��ֵ��BC�㹻��������Ϊ��ֵʱ�����滮��г�ȡ�����Сֵ����Сֵ�Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У���A��B��C���Եı߷ֱ�Ϊa��b��c����acosA=bsinb���� ![]() ����sinA+sinC�����ֵ�� ��
����sinA+sinC�����ֵ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijʯ�����Ż����ij�����������Ŀ���Ȩ�������ڸõ������������̽�˲��ּ��ھ���ȡ���˵������ϣ�����ȫ�濱̽ʱ�ں��Ű�����������þ�λ����ȫ�濱̽�����ڿ�̽һ�ھ��ķ��úܸߣ��������Ƶľ�λ��ԭ�о�λ�غϻ�ӽ��������þɾ��ĵ������ϣ����ش�����¾����Խ�Լ��̽���ã���̽�����������ϼ������

���ο���ʽ�ͼ�������  ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
��
��1��1��6�ž�λ�����Էֲ�������ǰ5�����ݣ�����![]() ����ûع�ֱ�߷���Ϊ
����ûع�ֱ�߷���Ϊ![]() ����
����![]() ��ֵ��������
��ֵ��������![]() ��Ԥ��ֵ��
��Ԥ��ֵ��
��2��������̽�¾�![]() ����ͨ��1��3��5��7�Ų�������ģ�
����ͨ��1��3��5��7�Ų�������ģ�![]() ��
�� ![]() ��ȷ��0.01������
��ȷ��0.01������ ��
��  ����
����![]() ��������10%ʱ��ʹ��λ����ӽ������оɾ�
��������10%ʱ��ʹ��λ����ӽ������оɾ�![]() ����������λ�ô����жϿɷ�ʹ�þɾ���
����������λ�ô����жϿɷ�ʹ�þɾ���
��3����������뿱̽��ȵı�ֵ![]() ������20�Ŀ�̽����Ϊ���ʾ�����ô��ԭ��6�ھ������⿱̽4�ھ�����̽���ʾ���
������20�Ŀ�̽����Ϊ���ʾ�����ô��ԭ��6�ھ������⿱̽4�ھ�����̽���ʾ���![]() �ķֲ�������ѧ����.
�ķֲ�������ѧ����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У���A��B��C���Եı߷ֱ�Ϊa��b��c���� ![]() asinA=��
asinA=�� ![]() b��c��sinB+��
b��c��sinB+�� ![]() c��b��sinC��
c��b��sinC��
��1�����A�Ĵ�С��
��2����a= ![]() ��cosB=
��cosB= ![]() ��DΪAC���е㣬��BD�ij���
��DΪAC���е㣬��BD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ƽ������ ![]() ��
�� ![]() ��
�� ![]() �����н�����ȷ�ĸ���Ϊ�� �� ����
�����н�����ȷ�ĸ���Ϊ�� �� ���� ![]()
![]() =
= ![]()
![]() ����
���� ![]() =
= ![]() ��
��
���� ![]() =��1��k����
=��1��k���� ![]() =����2��6����
=����2��6���� ![]() ��
�� ![]() ����k=��3��
����k=��3��
�۷������� ![]() ��
�� ![]() ����|
����| ![]() |=|
|=| ![]() |=|
|=| ![]() ��
�� ![]() |����
|���� ![]() ��
�� ![]() +
+ ![]() �ļн�Ϊ30�㣻
�ļн�Ϊ30�㣻
����֪���� ![]() ����
���� ![]() ��
�� ![]() �ļн�Ϊ��ǣ���ʵ���˵�ȡֵ��Χ��
�ļн�Ϊ��ǣ���ʵ���˵�ȡֵ��Χ�� ![]() ��
��
A.4��
B.3��
C.2��
D.1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() Ϊ����
Ϊ����![]() �����㣬
�����㣬 ![]() ��
��![]() �ĺ�����֮��Ϊ2.
�ĺ�����֮��Ϊ2.
��1����ֱ��![]() ��б�ʣ�
��б�ʣ�
��2����![]() ����
Ϊ����![]() ��һ�㣬����
��һ�㣬����![]() �ڵ�
�ڵ�![]() ����������ֱ��
����������ֱ��![]() ƽ�У���
ƽ�У���![]() ����ֱ��
����ֱ��![]() �ķ���.
�ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=asinxcosx�� ![]() acos2x+
acos2x+ ![]() a+b��a��0��
a+b��a��0��
��1��д�������ĵ����ݼ����䣻
��2����x��[0�� ![]() ]��f��x������Сֵ�ǩ�2�����ֵ��
]��f��x������Сֵ�ǩ�2�����ֵ�� ![]() ����ʵ��a��b��ֵ��
����ʵ��a��b��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����{an}����a2= ![]() ����an+1=3an��1��n��N*����
����an+1=3an��1��n��N*����
��1��������{an}��ͨ�ʽ�Լ�����{an}��ǰn���Sn�ı���ʽ��
��2��������ʽ ![]() ��m��n��N*���������ʵ��m��ȡֵ��Χ��
��m��n��N*���������ʵ��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com