
【题目】已知函数f(x)=lnx﹣tx+t.
(1)讨论f(x)的单调性;
(2)当t=2时,方程f(x)=m﹣ax恰有两个不相等的实数根x1,x2,证明:![]() .
.
【答案】(1)当t≤0时,f(x)在(0,+∞)上单调递增;当t>0时,f(x)在(0,![]() )上单调递增,在(
)上单调递增,在(![]() ,+∞)上单调递减;(2)证明见解析.
,+∞)上单调递减;(2)证明见解析.
【解析】
(1)求导后分![]() 和
和![]() 两种情况讨论极值点的大小关系以及导函数的正负,进而求得原函数的单调区间即可.
两种情况讨论极值点的大小关系以及导函数的正负,进而求得原函数的单调区间即可.
(2)代入![]() ,根据f(x)=m﹣ax,可得
,根据f(x)=m﹣ax,可得![]() 的两根分别为
的两根分别为![]() ,再消去
,再消去![]() 化简得到
化简得到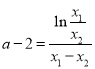 ,再代入所证的
,再代入所证的![]() ,换元令
,换元令![]() ,进而求导分析导数的正负以及原函数的单调性即可.
,进而求导分析导数的正负以及原函数的单调性即可.
(1)f(x)的定义域为(0,+∞),f′(x)![]() ,
,
当t≤0时,f′(x)>0恒成立,f(x)在(0,+∞)上单调递增,
当t>0时,令f′(x)>0,得0<x![]() ,令f′(x)<0,得x
,令f′(x)<0,得x![]() .
.
∴f(x)在(0,![]() )上单调递增,在(
)上单调递增,在(![]() ,+∞)上单调递减.
,+∞)上单调递减.
综上所述,当t≤0时,f(x)在(0,+∞)上单调递增;
当t>0时,f(x)在(0,![]() )上单调递增,在(
)上单调递增,在(![]() ,+∞)上单调递减.
,+∞)上单调递减.
(2)证明:由f(x)=m﹣ax,得lnx+(a﹣2)x+2﹣m=0.
令g(x)=lnx+(a﹣2)x+2,则g(x1)=g(x2)=m.
即lnx1+(a﹣2)x1=lnx2+(a﹣2)x2,
∴a﹣2 .
.
不妨设0<x1<x2,要证![]() ,
,
只需证![]() 2(2﹣a)
2(2﹣a) ,即证
,即证![]() .
.
令![]() (c>1),g(c)=2lnc﹣c
(c>1),g(c)=2lnc﹣c![]() ,
,
∵g′(c)![]() 0.
0.
∴g(c)在(1,+∞)上单调递减,则g(c)<g(1)=0.
故![]() 成立.
成立.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 为抛物线的焦点,
为抛物线的焦点,![]() 是过焦点的动弦,
是过焦点的动弦,![]() 是
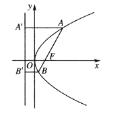
是![]() 两点在准线上的投影,如图所示,则下列论断正确的个数有( )
两点在准线上的投影,如图所示,则下列论断正确的个数有( )
①以![]() 为直径的圆与准线一定相切;
为直径的圆与准线一定相切;
②以![]() 为直径的圆与直线
为直径的圆与直线![]() 一定相切;
一定相切;
③以![]() 为直径的圆与
为直径的圆与![]() 轴一定相切;
轴一定相切;
④以![]() 为直径的圆与
为直径的圆与![]() 轴有可能相切
轴有可能相切
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某个微信群某次进行的抢红包活动中,群主所发红包的总金额为10元,被随机分配为2.49元、1.32元、2.19元、0.63元、3.37元共5份,供甲、乙等5人抢,每人只能抢一次,则甲、乙二人抢到的金额之和不低于4元的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足,an+1=an+1![]() ,a1=a,则一定存在a,使数列中( )
,a1=a,则一定存在a,使数列中( )
A.存在n∈N*,有an+1an+2<0
B.存在n∈N*,有(an+1﹣1)(an+2﹣1)<0
C.存在n∈N*,有![]()
D.存在n∈N*,有![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
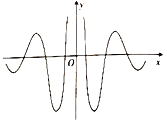
【题目】著名数学家华罗庚先生曾说过:“数缺形时少直观,形缺数时难入微数形结合百般好,隔裂分家万事休.”在数学的学习和研究中,我们经常用函数的图象来研究函数的性质,也经常用函数的解析式来琢磨函数的图象的特征,如某体育品牌的LOGO为![]() ,可抽象为如图所示的轴对称的优美曲线,下列函数中,其图象大致可“完美”局部表达这条曲线的函数是( )
,可抽象为如图所示的轴对称的优美曲线,下列函数中,其图象大致可“完美”局部表达这条曲线的函数是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图象的一条对称轴为
的图象的一条对称轴为![]() ,则下列结论中正确的是( )
,则下列结论中正确的是( )
A.![]() 是最小正周期为
是最小正周期为![]() 的奇函数
的奇函数
B.![]() 是
是![]() 图像的一个对称中心
图像的一个对称中心
C.![]() 在
在![]() 上单调递增
上单调递增
D.先将函数![]() 图象上各点的纵坐标缩短为原来的
图象上各点的纵坐标缩短为原来的![]() ,然后把所得函数图象再向左平移
,然后把所得函数图象再向左平移![]() 个单位长度,即可得到函数
个单位长度,即可得到函数![]() 的图象.
的图象.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知![]() 内接于圆O,AB是圆O的直径,四边形DBCE为平行四边形,F是CD的中点,
内接于圆O,AB是圆O的直径,四边形DBCE为平行四边形,F是CD的中点,
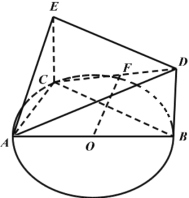
(1)证明:![]() 平面ADE;
平面ADE;
(2)若四边形DBCE为矩形,且四边形DBCE所在的平面与圆O所在的平面互相垂直,![]() ,AE与圆O所在的平面的线面角为60°.求二面角
,AE与圆O所在的平面的线面角为60°.求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com