
甲、乙两人各进行3次射击,甲每次击中目标的概率为 ,乙每次击中目标的概率为
,乙每次击中目标的概率为 ,两人间每次射击是否击中目标互不影响。
,两人间每次射击是否击中目标互不影响。
(1)求乙至多击中目标2次的概率;
(2)求甲恰好比乙多击中目标1次的概率。
科目:高中数学 来源: 题型:解答题
某种有奖销售的饮料,瓶盖内印有“奖励一瓶”或“谢谢购买”字样,购买一瓶若其瓶盖内印有“奖励一瓶”字样即为中奖,中奖概率为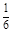 .甲、乙、丙三位同学每人购买了一瓶该饮料.
.甲、乙、丙三位同学每人购买了一瓶该饮料.
(1)求甲中奖且乙、丙都没有中奖的概率;
(2)求中奖人数ξ的分布列及数学期望Eξ.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某人上楼梯,每步上一阶的概率为 ,每步上二阶的概率为
,每步上二阶的概率为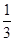 ,设该人从台阶下的平台开始出发,到达第
,设该人从台阶下的平台开始出发,到达第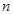 阶的概率为
阶的概率为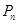 .
.
(1)求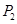 ;;
;;
(2)该人共走了5步,求该人这5步共上的阶数ξ的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某商场为吸引顾客消费推出一项优惠活动,活动规则如下:消费额每满100元可转动如图所示的转盘一次,并获得相应金额的返券,假定指针等可能地停在任一位置. 若指针停在 区域返券60元;停在
区域返券60元;停在 区域返券30元;停在
区域返券30元;停在 区域不返券. 例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.
区域不返券. 例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.
(1)若某位顾客消费128元,求返券金额不低于30元的概率;
(2)若某位顾客恰好消费280元,并按规则参与了活动,他获得返券的金额记为 (元),求随机变量
(元),求随机变量 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲打靶射击,有4发子弹,其中有一发是空弹(“空弹”即只有弹体没有弹头的子弹).
(1)如果甲只射击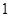 次,求在这一枪出现空弹的概率;
次,求在这一枪出现空弹的概率;
(2)如果甲共射击 次,求在这三枪中出现空弹的概率
次,求在这三枪中出现空弹的概率
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一车间生产A, B, C三种样式的LED节能灯,每种样式均有10W和30W两种型号,某天的产量如右表(单位:个)。按样式分层抽样的方法在这个月生产的灯泡中抽取100个,其中有A样式灯泡25个.
| 型号 | A样式 | B样式 | C样式 |
| 10W | 2000 | z | 3000 |
| 30W | 3000 | 4500 | 5000 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题15分)已知动圆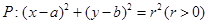 被y轴所截的弦长为2,被x轴分成两段弧,且弧长之比等于
被y轴所截的弦长为2,被x轴分成两段弧,且弧长之比等于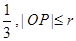 (其中
(其中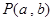 为圆心,O为坐标原点)。
为圆心,O为坐标原点)。
(1)求a,b所满足的关系式;
(2)点P在直线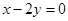 上的投影为A,求事件“在圆P内随机地投入一点,使这一点恰好在
上的投影为A,求事件“在圆P内随机地投入一点,使这一点恰好在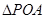 内”的概率的最大值
内”的概率的最大值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com