
【题目】已知直线系方程![]() (其中
(其中![]() 为参数).当
为参数).当![]() 时,直线
时,直线![]() 与两坐标轴所围成的三角形的面积为__________,若该直线系中的三条直线围成正三角形区域
与两坐标轴所围成的三角形的面积为__________,若该直线系中的三条直线围成正三角形区域![]() ,则区域
,则区域![]() 的面积为__________.
的面积为__________.
科目:高中数学 来源: 题型:
【题目】如图,已知双曲线 ![]() =1(a>0,b>0)的左右焦点分别为F1 , F2 , |F1F2|=4,P是双曲线右支上的一点,F2P与y轴交于点A,△APF1的内切圆在边PF1上的切点为Q,若|PQ|=1,则双曲线的离心率是( )
=1(a>0,b>0)的左右焦点分别为F1 , F2 , |F1F2|=4,P是双曲线右支上的一点,F2P与y轴交于点A,△APF1的内切圆在边PF1上的切点为Q,若|PQ|=1,则双曲线的离心率是( ) 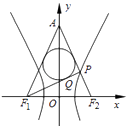
A.3
B.2
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() ,B(0,2),C(1,0),斜率为
,B(0,2),C(1,0),斜率为 ![]() 的直线l过点A,且l和以C为圆心的圆相切.
的直线l过点A,且l和以C为圆心的圆相切.
(1)求圆C的方程;
(2)在圆C上是否存在点P,使得 ![]() ,若存在,求出所有的点P的坐标;若不存在说明理由;
,若存在,求出所有的点P的坐标;若不存在说明理由;
(3)若不过C的直线m与圆C交于M,N两点,且满足CM,MN,CN的斜率依次为等比数列,求直线m的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在2017年初的时候,国家政府工作报告明确提出,2017年要坚决打好蓝天保卫战,加快解决燃煤污染问题,全面实施散煤综合治理.实施煤改电工程后,某县城的近六个月的月用煤量逐渐减少,6月至11月的用煤量如下表所示:

(1)由于某些原因, ![]() 中一个数据丢失,但根据6至9月份的数据得出少样本平均值是3.5,求出丢失的数据;
中一个数据丢失,但根据6至9月份的数据得出少样本平均值是3.5,求出丢失的数据;
(2)请根据6至9月份的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)现在用(2)中得到的线性回归方程中得到的估计数据与10月11月的实际数据的误差来判断该地区的改造项目是否达到预期,若误差均不超过0.3,则认为该地区的改造已经达到预期,否则认为改造未达预期,请判断该地区的煤改电项目是否达预期?(参考公式:线性回归方程![]() ,其中
,其中 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中有“今有五人分无钱,令上二人所得与下三人等,问各得几何?”.其意思为“已知甲、乙、丙、丁、戊五人分5钱,甲、乙两人所得与丙、丁、戊三人所得相同,且甲、乙、丙、丁、戊所得依次成等差数列,问五人各得多少钱?”这个问题中,甲所得为( )
A.![]() 钱
钱
B.![]() 钱
钱
C.![]() 钱
钱
D.![]() 钱
钱
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知点
中,已知点![]() 和
和![]() .
.
(![]() )若
)若![]() ,
, ![]() 是正方形一条边上的两个顶点,求这个正方形过顶点
是正方形一条边上的两个顶点,求这个正方形过顶点![]() 的两条边所在直线的方程;
的两条边所在直线的方程;
(![]() )若
)若![]() ,
, ![]() 是正方形一条对角线上的两个顶点,求这个正方形另外一条对角线所在直线的方程及其端点的坐标.
是正方形一条对角线上的两个顶点,求这个正方形另外一条对角线所在直线的方程及其端点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,△ABC是圆的内接三角形,∠BAC的平分线交圆于点D,交BC于E,过点B的圆的切线与AD的延长线交于点F,在上述条件下,给出下列四个结论:
①BD平分∠CBF;
②FB2=FDFA;
③AECE=BEDE;
④AFBD=ABBF.
所有正确结论的序号是( )
A.①②
B.③④
C.①②③
D.①②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行有奖促销活动,顾客购买一定金额商品后即可抽奖,每次抽奖都从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中,各随机摸出1个球,在摸出的2个球中,若都是红球,则获一等奖;若只有1个红球,则获二等奖;若没有红球,则不获奖.
(1)求顾客抽奖1次能获奖的概率;
(2)若某顾客有3次抽奖机会,记该顾客在3次抽奖中获一等奖的次数为x,求x的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2 ![]() sin(
sin( ![]() ωx)cos(
ωx)cos( ![]() ωx)+2cos2(
ωx)+2cos2( ![]() ωx)(ω>0),且函数f(x)的最小正周期为π.
ωx)(ω>0),且函数f(x)的最小正周期为π.
(1)求ω的值;
(2)求f(x)在区间 ![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com