
【题目】某学生对函数![]() 的性质进行研究,得出如下的结论:
的性质进行研究,得出如下的结论:
![]() 函数在
函数在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;
上单调递增;
![]() 点
点![]() 是函数图象的一个对称中心;
是函数图象的一个对称中心;
![]() 函数图象关于直线
函数图象关于直线![]() 对称;
对称;
![]() 存在常数
存在常数![]() ,使
,使![]() 对一切实数x均成立,
对一切实数x均成立,
其中正确命题的个数是( )
A.1B.2C.3D.4
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:高中数学 来源: 题型:
【题目】某学校为准备参加市运动会,对本校甲、乙两个田径队中![]() 名跳高运动员进行了测试,并用茎叶图表示出本次测试
名跳高运动员进行了测试,并用茎叶图表示出本次测试![]() 人的跳高成绩(单位:
人的跳高成绩(单位:![]() ).跳高成绩在
).跳高成绩在![]() 以上(包括
以上(包括![]() )定义为“合格”,成绩在
)定义为“合格”,成绩在![]() 以下(不包括
以下(不包括![]() )定义为“不合格”.鉴于乙队组队晚,跳高成绩相对较弱,为激励乙队队队,学校决定只有乙队中“合格”者才能参加市运动会开幕式旗林队.
)定义为“不合格”.鉴于乙队组队晚,跳高成绩相对较弱,为激励乙队队队,学校决定只有乙队中“合格”者才能参加市运动会开幕式旗林队.
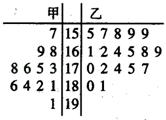
(1)求甲队队员跳高成绩的中位数;
(2)如果用分层抽样的方法从甲、乙两队所有的运动员中共抽取![]() 人,则
人,则![]() 人中“合格”与“不合格”的人数各为多少;
人中“合格”与“不合格”的人数各为多少;
(3)若从所有“合格”运动员中选取![]() 名,用
名,用![]() 表示所选运动员中能参加市运动会开幕式旗林队的人数,试求
表示所选运动员中能参加市运动会开幕式旗林队的人数,试求![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有下列四个命题:(1)一定存在直线![]() ,使函数
,使函数![]() 的图像与函数
的图像与函数![]() 的图像关于直线
的图像关于直线![]() 对称;(2)不等式:
对称;(2)不等式:![]() 的解集为
的解集为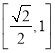 ;(3)已知数列
;(3)已知数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() ,则数列
,则数列![]() 一定是等比数列;(4)过抛物线
一定是等比数列;(4)过抛物线![]() 上的任意一点
上的任意一点![]() 的切线方程一定可以表示为
的切线方程一定可以表示为![]() .则正确命题的序号为_________________.
.则正确命题的序号为_________________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若对任意的正整数![]() ,总存在正整数
,总存在正整数![]() ,使得数列
,使得数列![]() 的前
的前![]() 项和
项和![]() ,则称
,则称![]() 是“回归数列”.
是“回归数列”.
(1)①前![]() 项和为
项和为![]() 的数列
的数列![]() 是否是“回归数列”?并请说明理由;
是否是“回归数列”?并请说明理由;
②通项公式为![]() 的数列
的数列![]() 是否是“回归数列”?并请说明理由;
是否是“回归数列”?并请说明理由;
(2)设![]() 是等差数列,首项
是等差数列,首项![]() ,公差
,公差![]() ,若
,若![]() 是“回归数列”,求
是“回归数列”,求![]() 的值;
的值;
(3)是否对任意的等差数列![]() ,总存在两个“回归数列”
,总存在两个“回归数列”![]() 和
和![]() ,使得
,使得![]() 成立,请给出你的结论,并说明理由.
成立,请给出你的结论,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由于受到网络电商的冲击,某品牌的洗衣机在线下的销售受到影响,承受了一定的经济损失,现将![]() 地区200家实体店该品牌洗衣机的月经济损失统计如图所示.
地区200家实体店该品牌洗衣机的月经济损失统计如图所示.
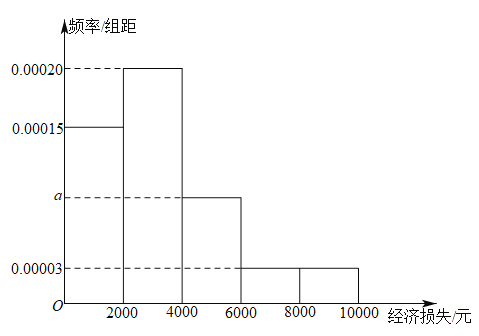
(1)求![]() 的值;
的值;
(2)求![]() 地区200家实体店该品牌洗衣机的月经济损失的众数以及中位数;
地区200家实体店该品牌洗衣机的月经济损失的众数以及中位数;
(3)不经过计算,直接给出![]() 地区200家实体店经济损失的平均数
地区200家实体店经济损失的平均数![]() 与6000的大小关系.
与6000的大小关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一款手游,页面上有一系列的伪装,其中隐藏了4个宝藏.如果你在规定的时间内找到了这4个宝藏,将会弹出下一个页面,这个页面仍隐藏了2个宝藏,若能在规定的时间内找到这2个宝藏,那么闯关成功,否则闯关失败,结束游戏;如果你在规定的时间内找到了3个宝藏,仍会弹出下一个页面,但这个页面隐藏了4个宝藏,若能在规定的时间内找到这4个宝藏,那么闯关成功,否则闯关失败,结束游戏;其它情况下,不会弹出下一个页面,闯关失败,并结束游戏.
假定你找到任何一个宝藏的概率为![]() ,且能否找到其它宝藏相互独立..
,且能否找到其它宝藏相互独立..
(1)求闯关成功的概率;
(2)假定你付1个Q币游戏才能开始,能进入下一个页面就能获得2个Q币的奖励,闯关成功还能获得另外4个Q币的奖励,闯关失败没有额外的奖励.求一局游戏结束,收益的Q币个数X的数学期望(收益=收入-支出).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com