
分析 (1)利用诱导公式即可化简得解.
(2)由已知,利用诱导公式可求sinα=-$\frac{1}{5}$,根据角的范围,利用同角三角函数基本关系式可求cosα,由(1)即可解得得解f(α)的值.
解答 (本题满分为10分)
解:(1)f(α)=$\frac{sin(π+α)sin(α+\frac{π}{2})}{cos(α-\frac{π}{2})}$=$\frac{(-sinα)cosα}{sinα}$=-cosα…5分
(2)∵α是第三象限角,cos(α+$\frac{π}{2}$)=-sinα=$\frac{1}{5}$,
∴sinα=-$\frac{1}{5}$,
∴cosα=-$\sqrt{1-si{n}^{2}α}$=-$\frac{2\sqrt{6}}{5}$.
∴f(α)=-cosα=$\frac{2\sqrt{6}}{5}$…10分
点评 本题主要考查了诱导公式,同角三角函数基本关系式在三角函数化简求值中的应用,考查了计算能力和转化思想,解题时要注意角的范围,属于基础题.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | c<a<b | C. | b<a<c | D. | c<b<a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
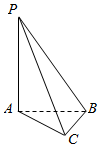 如图,在四面体P-ABC中,PA、AB、BC两两垂直,且AB=$\sqrt{6}$,BC=$\sqrt{2}$,则二面角B-AP-C的大小为( )
如图,在四面体P-ABC中,PA、AB、BC两两垂直,且AB=$\sqrt{6}$,BC=$\sqrt{2}$,则二面角B-AP-C的大小为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源:2015-2016学年江苏泰兴中学高二上学期期末数学(文)试卷(解析版) 题型:填空题
下列四个命题:①一个命题的逆命题为真,则它的逆否命题一定为真;②命题“设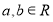 ,若
,若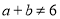 ,则
,则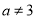 或
或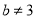 ”是一个假命题;③“
”是一个假命题;③“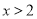 ”是“
”是“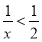 ”的充分不必要条件;④一个命题的否命题为真,则它的逆命题一定为真.其中不正确的命题是 .(写出所有不正确命题的序号)
”的充分不必要条件;④一个命题的否命题为真,则它的逆命题一定为真.其中不正确的命题是 .(写出所有不正确命题的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com