
����Ŀ��ij���������ȷ����ˣ��������û���������.Ϊ�˸��õ����ۣ������ժ����![]() ����Ƚ��в��أ��������ֲ�������
����Ƚ��в��أ��������ֲ�������![]() �ڣ���λ���ˣ���ͳ����������������Ƶ�ʷֲ�ֱ��ͼ����ͼ��ʾ��
�ڣ���λ���ˣ���ͳ����������������Ƶ�ʷֲ�ֱ��ͼ����ͼ��ʾ��
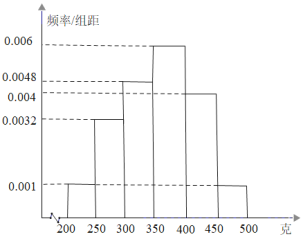
��1�����ֲ�����ķ�������������![]() ��
��![]() ������������ȡ
������������ȡ![]() �����ٴ���
�����ٴ���![]() ������������
������������![]() ��������
��������![]() ���������������
�������������С��![]() �˵ĸ��ʣ�
�˵ĸ��ʣ�
��2���Ը������ݵ��м���ֵ�����������ݵ�ƽ��ˮƽ����Ƶ�ʴ������ʣ���֪�ù���������ϴ�Լ����![]() ����ȴ����ۣ�ij������������չ��������ף�������Ⱦ���
����ȴ����ۣ�ij������������չ��������ף�������Ⱦ���![]() Ԫ/ǧ���չ����ң�����
Ԫ/ǧ���չ����ң�����![]() �˵������
�˵������![]() Ԫ/���չ������ڻ����
Ԫ/���չ������ڻ����![]() �˵���
�˵���![]() Ԫ/���չ�.��ͨ������Ϊ�ù�ѡ��������õķ���.
Ԫ/���չ�.��ͨ������Ϊ�ù�ѡ��������õķ���.
���ο����ݣ�![]() ��
��
���𰸡���1��![]() ����2��������
����2��������
��������
��1���ɷֲ����֪������Ϊ![]() ��
��![]() ������и���ȡ
������и���ȡ![]() ����
����![]() ���������оٷ�����ʣ�
���������оٷ�����ʣ�
��2���ֱ����ס��ҷ������������棬�Ƚϼ��ɵõ���.
��1��������֪�����![]() ��
��![]() �ı���Ϊ
�ı���Ϊ![]() ����Ӧ�ֱ�������Ϊ
����Ӧ�ֱ�������Ϊ![]() ��
��
![]() ������г�ȡ
������г�ȡ![]() ����
����![]() ��.
��.
�dz�ȡ������![]() ��Ϊ
��Ϊ![]() ��������
��������![]() ��Ϊ
��Ϊ![]() �������
�������![]() �������
�������
�����ȡ![]() ���ķ�����������
���ķ�����������![]() �֣�
�֣�
![]() ������
������![]() ���������������
�������������С��![]() �˵ķ���
�˵ķ���
��![]() �֣���
�֣���![]() �������������С��
�������������С��![]() �˵ĸ���Ϊ
�˵ĸ���Ϊ![]() .
.
��2�������Ҹ��ã��������£�
��Ƶ�ʷֲ�ֱ��ͼ֪![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
![]() ��Ƶ�ʷֱ�Ϊ
��Ƶ�ʷֱ�Ϊ![]() .
.
���ü�����������Ϊ![]() Ԫ��
Ԫ��
�����ҷ�������ȵ���![]() �˵���
�˵���![]() ����������
����������![]() ��
��
����![]() ��.��������Ϊ
��.��������Ϊ![]() Ԫ
Ԫ
���ԣ��ҷ���������ߣ�ѡ����.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ����
����![]() ��
��
��1��������![]() ��ͨ�ʽ��
��ͨ�ʽ��
��2����![]() ������
������![]() ��ǰ
��ǰ![]() ���Ϊ
���Ϊ![]() ����
����![]() ��
��
��3����![]() ���ʣ��Ƿ���ڷ�������
���ʣ��Ƿ���ڷ�������![]() ��ʹ����
��ʹ����![]() Ϊ�������У������ڣ����
Ϊ�������У������ڣ����![]() ��ֵ���������ڣ���˵�����ɣ�
��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��![]() x2+ax+lnx��a��R��
x2+ax+lnx��a��R��
��1�����ۺ���f��x���ĵ����ԣ�
��2����f��x������������ֵ��x1��x2��|x1��x2|![]() ����|f��x1����f��x2��|�����ֵ.
����|f��x1����f��x2��|�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��2011�굽2018��μ�����Լ������Լ�����Զ���üӷֵ�ѧ����ÿλѧ��ֻ�ܲμ�����Լ������Լ���е�һ�ֿ��ԣ���������ͨ�����±���ӳ����.��Ϊ�˷�����㣬��2011����Ϊ1��2012����Ϊ2���������ƣ�
��� | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
���� | 2 | 3 | 4 | 4 | 7 | 7 | 6 | 6 |
��1���������������У�μ�����Լ������Լ�����Զ���üӷֵ�ѧ����������λ���ͷ��
��2�����������������ݣ�������С���˷����![]() ��
��![]() ֮������Իع鷽�̣�������Ԥ���У2019��μ�����Լ������Լ�����Զ���üӷֵ�ѧ������.�����Ҫ��������������λ��
֮������Իع鷽�̣�������Ԥ���У2019��μ�����Լ������Լ�����Զ���üӷֵ�ѧ������.�����Ҫ��������������λ��
�ο���ʽ�� .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ������
������![]() ����
����![]() ��
��![]() ��
��![]() ��
��![]() Ϊ
Ϊ![]() �е㣬
�е㣬![]() ��
��
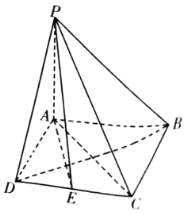
��1����֤��ƽ��![]() ƽ��
ƽ��![]() ��
��
��2����![]() ��������
��������![]() ������ֵ��
������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() ����������
����������![]() �ڵ�
�ڵ�![]() ��������б��Ϊ
��������б��Ϊ![]() ��ֱ��
��ֱ��![]() �������߽���
�������߽���![]() ���㣨��
���㣨��![]() �ڵ�
�ڵ�![]() ��ࣩ����ֱ��
��ࣩ����ֱ��![]() ��ֱ��ֱ��
��ֱ��ֱ��![]() ��
��
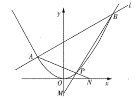
��1����֤��ֱ��![]() �����㣬������������ꣻ
�����㣬������������ꣻ
��2����ͼ��ֱ��![]() ��
��![]() ���ڵ�
���ڵ�![]() ��ֱ��
��ֱ��![]() ��
��![]() ���ڵ㣬��
���ڵ㣬��![]() �����ֵ��
�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���в������ڼ䣬ij���������߲��Ÿ��������Ʒ������Ƽ�����������ҩ��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��ʹ���ǻ������걸�ģ������Ҹ�Ⱦ���߰��涨���õ���ҩ������.�����ڹ���������ҩ����йز������г������������±���ʾ�������е����ݶ���һ���Ƴ̼ƣ�
��ʹ���ǻ������걸�ģ������Ҹ�Ⱦ���߰��涨���õ���ҩ������.�����ڹ���������ҩ����йز������г������������±���ʾ�������е����ݶ���һ���Ƴ̼ƣ�
|
|
|
|
���ۣ���λ��Ԫ�� | 600 | 1000 | 800 |
������ |
|
|
|
�г�ʹ��������λ���ˣ� | 305 | 122 | 183 |
���Ӹ�Ⱦ��������ȡһ�ˣ�������һ���Ƴ̱������ĸ��ʴ�Լ�Ƕ��٣�
�����Թ���ÿ����Ⱦ������һ���Ƴ̵�ҩ�����Ʒ���ƽ���Ƕ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У���ԲC��![]() (a��b��0)��������Ϊ
(a��b��0)��������Ϊ![]() ���ҽ��㵽���ߵľ���Ϊ3.
���ҽ��㵽���ߵľ���Ϊ3.
��1������ԲC�ı����̣�
��2������P(0��1)��ֱ��l����ԲC��������A��B.��֪����ԲC�ϴ��ڵ�Q��ʹ���ı���OAQB��ƽ���ı��Σ���Q������.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com