
【题目】如图所示,在四棱锥![]() 中,底面ABCD是正方形,AC与BD交于点O,
中,底面ABCD是正方形,AC与BD交于点O,![]() 底面ABCD,F为BE的中点,
底面ABCD,F为BE的中点,![]() .
.
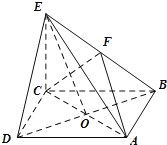
(1)求证:![]() 平面ACF;
平面ACF;
(2)求BE与平面ACE的所成角的正切值;
(3)在线段EO上是否存在点G,使CG![]() 平面BDE ?若存在,求出EG:EO的值,若不存在,请说明理由.
平面BDE ?若存在,求出EG:EO的值,若不存在,请说明理由.
【答案】(1)见解析; (2)![]() ;(3)1:2.
;(3)1:2.
【解析】
(1)连接OF,根据三角形中位线得线线平行,再根据线面平行判定定理得结果,(2)先根据线面垂直得线面角,再解直角三角形得结果,(3)取EO中点G,利用面面垂直判定与性质定理证得结果.
(1)连接OF.由ABCD是正方形可知,点O为BD中点.
又F为BE的中点,所以OF∥DE.
又OF面ACF,DE面ACF,
所以DE∥平面ACF.
(2)证明:由EC⊥底面ABCD,BD底面ABCD,
∴EC⊥BD,
由ABCD是正方形可知,AC⊥BD,
又AC∩EC=C,AC、E平面ACE,
∴BD⊥平面ACE,即![]() 就是所求角,
就是所求角,
因为![]()
故所正切值为![]() .
.
(3)在线段EO上存在点G,使CG⊥平面BDE.理由如下:
取EO中点G,连接CG,
在四棱锥EABCD中,AB=2√CE,CO=2√2AB=CE,
∴CG⊥EO.
由(2)可知,BD⊥平面ACE,而BD平面BDE,
∴平面ACE⊥平面BDE,且平面ACE∩平面BDE=EO,
∵CG⊥EO,CG平面ACE,
∴CG⊥平面BDE
故在线段EO上存在点G,使CG⊥平面BDE.
由G为EO中点,得EG:EO=1:2.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:
【题目】如图,△ABC是边长为4的等边三角形,△ABD是等腰直角三角形,AD⊥BD,平面ABC⊥平面ABD,且EC⊥平面ABC,EC=2.
(1)证明:DE∥平面ABC;
(2)证明:AD⊥BE.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}(n=1,2,3,4,5)满足a1=a5=0,且当2≤k≤5时,(ak﹣ak﹣1)2=1,令S=![]() , 则S不可能的值是( )
, 则S不可能的值是( )
A.4
B.0
C.1
D.-4
查看答案和解析>>
科目:高中数学 来源: 题型:
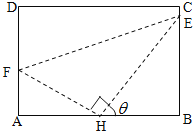
【题目】如图,某污水处理厂要在一个矩形污水处理池![]() 的池底水平铺设污水净化管道(
的池底水平铺设污水净化管道(![]() ,
,![]() 是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口
是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口![]() 是
是![]() 的中点,
的中点,![]() 分别落在线段
分别落在线段![]() 上.已知
上.已知![]() 米,
米,![]() 米,记
米,记![]() .
.
(1)试将污水净化管道的长度![]() 表示为
表示为![]() 的函数,并写出定义域;
的函数,并写出定义域;
(2)若![]() ,求此时管道的长度
,求此时管道的长度![]() ;
;
(3)当![]() 取何值时,污水净化效果最好?并求出此时管道的长度.
取何值时,污水净化效果最好?并求出此时管道的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,已知曲线
,已知曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 平行
平行
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)是否存在自然数![]() ,使得方程
,使得方程![]() 在
在![]() 内存在唯一的根?如果存在,求出
内存在唯一的根?如果存在,求出![]() ;如果不存在,请说明理由。
;如果不存在,请说明理由。
(Ⅲ)设函数![]() (
(![]() 表示
表示![]() 中的较小者),求
中的较小者),求![]() 的最大值。
的最大值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在区间[a,b]上的连续函数y=f(x),如果![]() ,使得
,使得![]() ,则称
,则称![]() 为区间[a,b]上的“中值点”,下列函数:
为区间[a,b]上的“中值点”,下列函数:
①![]() ; ②
; ②![]() ; ③
; ③![]() ; ④
; ④![]() 中,在区间[O,1]上“中值点”多于一个的函数序号为( )
中,在区间[O,1]上“中值点”多于一个的函数序号为( )
A. ①② B. ①③ C. ②③ D. ①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).在以原点
为参数).在以原点![]() 为极点,
为极点,![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com