
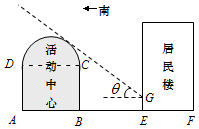
 如图所示,某街道居委会拟在EF地段的居民楼正南方向的空白地段AE上建一个活动中心,其中AE=30米.活动中心东西走向,与居民楼平行.从东向西看活动中心的截面图的下部分是长方形ABCD,上部分是以DC为直径的半圆.为了保证居民楼住户的采光要求,活动中心在与半圆相切的太阳光线照射下落在居民楼上的影长GE不超过2.5米,其中该太阳光线与水平线的夹角θ满足$tanθ=\frac{3}{4}$.
如图所示,某街道居委会拟在EF地段的居民楼正南方向的空白地段AE上建一个活动中心,其中AE=30米.活动中心东西走向,与居民楼平行.从东向西看活动中心的截面图的下部分是长方形ABCD,上部分是以DC为直径的半圆.为了保证居民楼住户的采光要求,活动中心在与半圆相切的太阳光线照射下落在居民楼上的影长GE不超过2.5米,其中该太阳光线与水平线的夹角θ满足$tanθ=\frac{3}{4}$.分析 (1)以点A为坐标原点,AB所在直线为x轴,建立平面直角坐标系.设太阳光线所在直线方程为$y=-\frac{3}{4}x+b$,利用直线与圆相切,求出直线方程,令x=30,得EG=1.5米<2.5米,即可得出结论;
(2)欲使活动中心内部空间尽可能大,则影长EG恰为2.5米,即可求出截面面积最大
解答 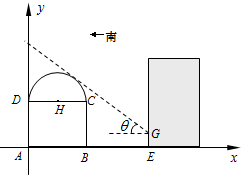 解:如图所示,以点A为坐标原点,AB所在直线为x轴,建立平面直角坐标系.
解:如图所示,以点A为坐标原点,AB所在直线为x轴,建立平面直角坐标系.
(1)因为AB=18,AD=6,所以半圆的圆心为H(9,6),
半径r=9.设太阳光线所在直线方程为$y=-\frac{3}{4}x+b$,
即3x+4y-4b=0,…(2分)
则由$\frac{|27+24-4b|}{{\sqrt{{3^2}+{4^2}}}}=9$,
解得b=24或$b=\frac{3}{2}$(舍).
故太阳光线所在直线方程为$y=-\frac{3}{4}x+24$,…(5分)
令x=30,得EG=1.5米<2.5米.
所以此时能保证上述采光要求…(7分)
(2)设AD=h米,AB=2r米,则半圆的圆心为H(r,h),半径为r.
欲使活动中心内部空间尽可能大,则影长EG恰为2.5米,则此时点G为(30,2.5),
设过点G的上述太阳光线为l1,则l1所在直线方程为y-$\frac{5}{2}$=-$\frac{3}{4}$(x-30),
即3x+4y-100=0…(10分)
由直线l1与半圆H相切,得$r=\frac{|3r+4h-100|}{5}$.
而点H(r,h)在直线l1的下方,则3r+4h-100<0,
即$r=-\frac{3r+4h-100}{5}$,从而h=25-2r…(13分)
又$S=2rh+\frac{1}{2}π{r^2}=2r(25-2r)+\frac{3}{2}×{r^2}$=$-\frac{5}{2}{r^2}+50r=-\frac{5}{2}{(r-10)^2}+250≤250$.
当且仅当r=10时取等号.
所以当AB=20米且AD=5米时,可使得活动中心的截面面积最大…(16分)
点评 本题考查利用数学知识解决实际问题,考查直线与圆的位置关系,考查配方法的运用,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com