
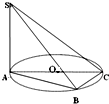
 如图,AC为圆O的直径,B为圆周上不与A、C重合的点,SA⊥圆O所在的平面,连接SB、SC、AB、BC,则图中直角三角形的个数是________.
如图,AC为圆O的直径,B为圆周上不与A、C重合的点,SA⊥圆O所在的平面,连接SB、SC、AB、BC,则图中直角三角形的个数是________. 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:
 如图,某城市设立以城中心O为圆心、r公里为半径的圆形保护区,从保护区边缘起,在城中心O正东方向上有一条高速公路PB、西南方向上有一条一级公路QC,现要在保护区边缘PQ弧上选择一点A作为出口,建一条连接两条公路且与圆O相切的直道BC.已知通往一级公路的道路AC每公里造价为a万元,通往高速公路的道路AB每公里造价是m2a万元,其中a,r,m为常数,设∠POA=θ,总造价为y万元.
如图,某城市设立以城中心O为圆心、r公里为半径的圆形保护区,从保护区边缘起,在城中心O正东方向上有一条高速公路PB、西南方向上有一条一级公路QC,现要在保护区边缘PQ弧上选择一点A作为出口,建一条连接两条公路且与圆O相切的直道BC.已知通往一级公路的道路AC每公里造价为a万元,通往高速公路的道路AB每公里造价是m2a万元,其中a,r,m为常数,设∠POA=θ,总造价为y万元.
| ||||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
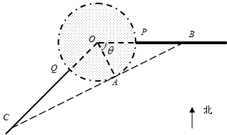 如图,某城市设立以城中心O为圆心、r公里为半径的圆形保护区,从保护区边缘起,在城中心O正东方向上有一条高速公路PB、西南方向上有一条一级公路QC,现要在保护区边缘PQ弧上选择一点A作为出口,建一条连接两条公路且与圆O相切的直道BC.已知通往一级公路的道路AC每公里造价为a万元,通往高速公路的道路AB每公里造价是m2a万元,其中a,r,m为常数,设∠POA=θ,总造价为y万元.
如图,某城市设立以城中心O为圆心、r公里为半径的圆形保护区,从保护区边缘起,在城中心O正东方向上有一条高速公路PB、西南方向上有一条一级公路QC,现要在保护区边缘PQ弧上选择一点A作为出口,建一条连接两条公路且与圆O相切的直道BC.已知通往一级公路的道路AC每公里造价为a万元,通往高速公路的道路AB每公里造价是m2a万元,其中a,r,m为常数,设∠POA=θ,总造价为y万元.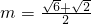 时,如何确定A点的位置才能使得总造价最低?
时,如何确定A点的位置才能使得总造价最低?查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省宿迁市沭阳县高一(下)期中数学试卷(解析版) 题型:解答题
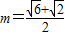 时,如何确定A点的位置才能使得总造价最低?
时,如何确定A点的位置才能使得总造价最低?
查看答案和解析>>
科目:高中数学 来源:陕西省宝鸡中学2010届高三适应性训练(数学理) 题型:填空题
A.(参数方程与极坐标)
直线 与直线
与直线 的夹角大小为
的夹角大小为
 B.(不等式选讲)要使关于x的不等式
B.(不等式选讲)要使关于x的不等式 在实数
在实数
范围内有解,则A的取值范围是
C.(几何证明选讲) 如图所示,在圆O中,AB是圆O的直
径AB =8,E为OB.的中点,CD过点E且垂直于AB,
EF⊥AC,则
CF•CA=
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com