
分析 本题考查的知识点是几何概型,由于函数cos$\frac{πx}{2}$是一个偶函数,故可研究出cos$\frac{πx}{2}$的值介于0到0.5之间对应线段的长度,再将其代入几何概型计算公式进行求解.
解答 解:由于函数y=cos$\frac{πx}{2}$是一个偶函数,可将问题转化为在区间[0,1]上随机取一个数x,则cos$\frac{πx}{2}$的值介于0到$\frac{1}{2}$之间的概率
在区间[0,1]上随机取一个数x,
即x∈[0,1]时,要使cos$\frac{πx}{2}$的值介于0到0.5之间,
需使$\frac{π}{3}$≤$\frac{πx}{2}$≤$\frac{π}{2}$
∴$\frac{2}{3}$≤x≤1,区间长度为$\frac{1}{3}$,
由几何概型知 cos$\frac{πx}{2}$的值介于0到0.5之间的概率为$\frac{1}{3}$.
故答案为:$\frac{1}{3}$.
点评 几何概型的概率估算公式中的“几何度量”,可以为线段长度、面积、体积等,而且这个“几何度量”只与“大小”有关,而与形状和位置无关.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m⊥n,n?α,则m⊥α | B. | 若m∥α,n∥α,则m∥n | C. | 若m⊥α,n∥m,则n⊥α | D. | 若α⊥γ,β⊥γ,则α∥β |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
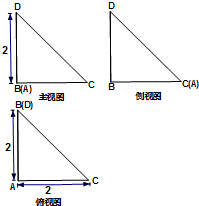 如图所示是三棱锥D-ABC的三视图,若在三棱锥的直观图中,点O为线段BC的中点,则异面直线DC与AB所成角的余弦值等于( )
如图所示是三棱锥D-ABC的三视图,若在三棱锥的直观图中,点O为线段BC的中点,则异面直线DC与AB所成角的余弦值等于( )| A. | $\frac{{\sqrt{6}}}{6}$ | B. | $\frac{{\sqrt{6}}}{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{5}}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ④ | D. | ①②③ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
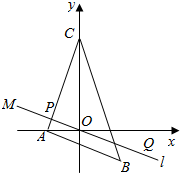 如图所示,已知A(-2,0),B(2,-2),C(0,5),过点M(-4,2)且平行于AB的直线l将△ABC分成两部分,求此两部分面积的比值.
如图所示,已知A(-2,0),B(2,-2),C(0,5),过点M(-4,2)且平行于AB的直线l将△ABC分成两部分,求此两部分面积的比值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com