
 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:
| A、a,b都能被7整除 |
| B、a,b不都能被7整除 |
| C、a,b至少有一个能被7整除 |
| D、a,b至多有一个能被7整除 |
查看答案和解析>>
科目:高中数学 来源: 题型:
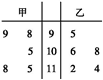 在某中学举行的跳高比赛选拨赛中,甲和乙进行了5次比赛,他们的成绩用如图所示的茎叶图表示,则下列说法正确的是( )
在某中学举行的跳高比赛选拨赛中,甲和乙进行了5次比赛,他们的成绩用如图所示的茎叶图表示,则下列说法正确的是( )| A、甲的平均成绩比乙的平均成绩高,甲比乙成绩稳定 |
| B、甲的平均成绩比乙的平均成绩低,乙比甲成绩稳定 |
| C、甲的平均成绩与乙的平均成绩一样,但甲比乙成绩稳定 |
| D、甲的平均成绩与乙的平均成绩一样,但乙比甲成绩稳定 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 6 |
A、(0,
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、34种 | B、35种 |
| C、120种 | D、140种 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 满 意 | 不满意 | 合 计 | |
| 男 生 | 50 | ||
| 女 生 | 15 | ||
| 合 计 | 100 |
| 4 |
| 5 |
| A、在犯错误的概率不超过0.1%的情况下,有把握说学生对新课程改革工作的满意情况与性别有关 |
| B、在犯错误的概率不超过0.1%的情况下,有把握说学生对新课程改革工作的满意情况与性别无关 |
| C、在犯错误的概率不超过0.5%的情况下,有把握说学生对新课程改革工作的满意情况与性别有关 |
| D、在犯错误的概率不超过0.5%的情况下,有把握说学生对新课程改革工作的满意情况与性别无关 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com