
【题目】在矩形ABCD中,AB=1,AD=2,动点P在以点C为圆心且与BD相切的圆上.若 ![]() =λ
=λ ![]() +μ
+μ ![]() ,则λ+μ的最大值为( )
,则λ+μ的最大值为( )
A.3
B.2 ![]()
C.![]()
D.2
【答案】A
【解析】解:如图:以A为原点,以AB,AD所在的直线为x,y轴建立如图所示的坐标系,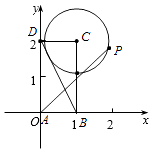
则A(0,0),B(1,0),D(0,2),C(1,2),
∵动点P在以点C为圆心且与BD相切的圆上,
设圆的半径为r,
∵BC=2,CD=1,
∴BD= ![]() =
= ![]()
∴ ![]() BCCD=
BCCD= ![]() BDr,
BDr,
∴r= ![]() ,
,
∴圆的方程为(x﹣1)2+(y﹣2)2= ![]() ,
,
设点P的坐标为( ![]() cosθ+1,
cosθ+1, ![]() sinθ+2),
sinθ+2),
∵ ![]() =λ
=λ ![]() +μ
+μ ![]() ,
,
∴( ![]() cosθ+1,
cosθ+1, ![]() sinθ﹣2)=λ(1,0)+μ(0,2)=(λ,2μ),
sinθ﹣2)=λ(1,0)+μ(0,2)=(λ,2μ),
∴ ![]() cosθ+1=λ,
cosθ+1=λ, ![]() sinθ+2=2μ,
sinθ+2=2μ,
∴λ+μ= ![]() cosθ+
cosθ+ ![]() sinθ+2=sin(θ+φ)+2,其中tanφ=2,
sinθ+2=sin(θ+φ)+2,其中tanφ=2,
∵﹣1≤sin(θ+φ)≤1,
∴1≤λ+μ≤3,
故λ+μ的最大值为3,
故选:A


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知公比小于1的等比数列{an}的前n项和为Sn , a1= ![]() ,且13a2=3S3(n∈N*).
,且13a2=3S3(n∈N*).
(1)求数列{an}的通项公式;
(2)设bn=log3(1﹣Sn+1),若 ![]() +
+ ![]() +…+
+…+ ![]() =
= ![]() ,求n.
,求n.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2x,过点(2,0)的直线l交C与A,B两点,圆M是以线段AB为直径的圆.
(Ⅰ)证明:坐标原点O在圆M上;
(Ⅱ)设圆M过点P(4,﹣2),求直线l与圆M的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某“双一流A类”大学就业部从该校2018年已就业的大学本科毕业生中随机抽取了100人进行问卷调查,其中一项是他们的月薪收入情况,调查发现,他们的月薪收入在人民币1.65万元到2.35万元之间,根据统计数据分组,得到如下的频率分布直方图:

(1)为感谢同学们对这项调查工作的支持,该校利用分层抽样的方法从样本的前两组中抽出6人,各赠送一份礼品,并从这6人中再抽取2人,各赠送某款智能手机1部,求获赠智能手机的2人月薪都不低于1.75万元的概率;
(2)同一组数据用该区间的中点值作代表.
(i)求这100人月薪收入的样本平均数![]() 和样本方差
和样本方差![]() ;
;
(ii)该校在某地区就业的2018届本科毕业生共50人,决定于2019国庆长假期间举办一次同学联谊会,并收取一定的活动费用,有两种收费方案:
方案一:设![]() ,月薪落在区间
,月薪落在区间![]() 左侧的每人收取400元,月薪落在区间
左侧的每人收取400元,月薪落在区间![]() 内的每人收到600元,月薪落在区间
内的每人收到600元,月薪落在区间![]() 右侧的每人收取800元.
右侧的每人收取800元.
方案二:按每人一个月薪水的3%收取;用该校就业部统计的这100人月薪收入的样本频率进行估算,哪一种收费方案能收到更多的费用?
参考数据:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于给定的正整数k,若数列{an}满足:an﹣k+an﹣k+1+…+an﹣1+an+1+…an+k﹣1+an+k=2kan对任意正整数n(n>k)总成立,则称数列{an}是“P(k)数列”.
(Ⅰ)证明:等差数列{an}是“P(3)数列”;
(Ⅱ)若数列{an}既是“P(2)数列”,又是“P(3)数列”,证明:{an}是等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在同一个平面内,向量 ![]() ,
, ![]() ,
, ![]() 的模分别为1,1,
的模分别为1,1, ![]() ,
, ![]() 与
与 ![]() 的夹角为α,且tanα=7,
的夹角为α,且tanα=7, ![]() 与
与 ![]() 的夹角为45°.若
的夹角为45°.若 ![]() =m
=m ![]() +n
+n ![]() (m,n∈R),则m+n= .
(m,n∈R),则m+n= . 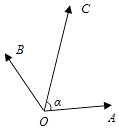
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某园林基地培育了一种新观赏植物,经过了一年的生长发育,技术人员从中抽取了部分植株的高度(单位:厘米)作为样本(样本容量为![]() )进行统计,按
)进行统计,按![]()
![]() 分组做出频率分布直方图,并作出样本高度的茎叶图(图中仅列出了高度在
分组做出频率分布直方图,并作出样本高度的茎叶图(图中仅列出了高度在![]() 的数据).
的数据).

(1)求样本容量![]() 和频率分布直方图中的
和频率分布直方图中的![]()
(2)在选取的样本中,从高度在80厘米以上(含80厘米)的植株中随机抽取3株,设随机变量![]() 表示所抽取的3株高度在
表示所抽取的3株高度在 ![]() 内的株数,求随机变量
内的株数,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com