解法(一):(1)设A(x
1,
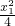
),
由x
2=4y,得:y′=

,∴k
PA=
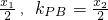
∵

=0,
∴PA⊥PB,∴x
1x
2=-4.(4分)
直线PA的方程是:y-
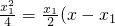
)即y=
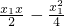
①
同理,直线PB的方程是:y=
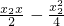
②,(6分)
由①②得:

∴点P的轨迹方程是y=-1(x∈R).(8分)
(2)由(1)得:
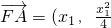
-1),
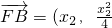
-1),P(

,-1)
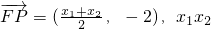
=-4,
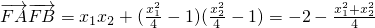
(
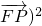
+2,
所以
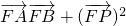
=0
故存在λ=1使得
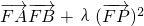
=0.(14分)
解法(二):(1)∵直线PA、PB与抛物线相切,且

=0,
∴直线PA、PB的斜率均存在且不为0,且PA⊥PB,
设PA的直线方程是y=kx+m(k,m∈R,k≠0)
由
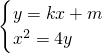
得:x
2-4kx-4m=0.(4分)
∴△=16k
2+16m=0即m=-k
2即直线PA的方程是:y=kx-k
2同理可得直线PB的方程是:y=-
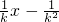
,(6分)
由
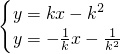
得:
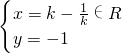
故点P的轨迹方程是y=-1(x∈R).(8分)
(2)由(1)得:A(2k,k
2),B(-

,
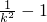
),
∴
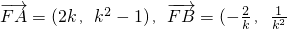
-1),
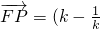
,-2)
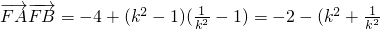
).
故存在λ=1使得
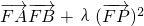
=0.(14分)
分析:法一:(1)设A(x
1,
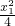
),由x
2=4y,得:y′=

,由此推导出直线PA的方程是:y=
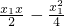
.同理,直线PB的方程是:y=
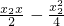
.由此能求出点P的轨迹方程.
(2)由
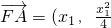
-1),
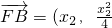
-1),得P(

,-1)
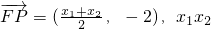
=-4,
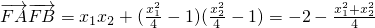
(
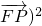
+2,由此能推导出存在λ=1使得
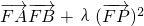
=0.
法二:(1)由直线PA、PB与抛物线相切,且

=0,设PA的直线方程是y=kx+m(k,m∈R,k≠0),由
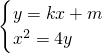
得:x
2-4kx-4m=0,△=16k
2+16m=0,得到直线PA的方程是:y=kx-k
2.同理可得直线PB的方程是:y=-
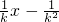
.由此能求出P的轨迹方程.
(2)由A(2k,k
2),B(-

,
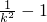
),知
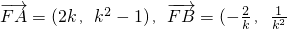
-1),
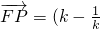
,-2),由此能推导出存在λ=1使得
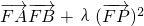
=0.
点评:通过几何量的转化考查用待定系数法求曲线方程的能力,通过直线与圆锥曲线的位置关系处理,考查学生的运算能力.通过向量与几何问题的综合,考查学生分析转化问题的能力,探究研究问题的能力,并体现了合理消元,设而不解的代数变形的思想.本题有一定的探索性.综合性强,难度大,易出错.

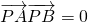 .
.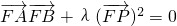 ?若存在,求出λ的值,若不存在,请说明理由.
?若存在,求出λ的值,若不存在,请说明理由.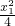 ),
), ,∴kPA=
,∴kPA=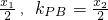 ∵
∵ =0,
=0,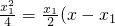 )即y=
)即y=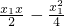 ①
①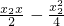 ②,(6分)
②,(6分)
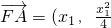 -1),
-1),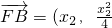 -1),P(
-1),P( ,-1)
,-1)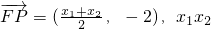 =-4,
=-4,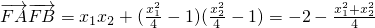 (
(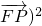 +2,
+2,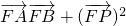 =0
=0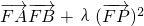 =0.(14分)
=0.(14分) =0,
=0,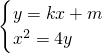 得:x2-4kx-4m=0.(4分)
得:x2-4kx-4m=0.(4分)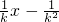 ,(6分)
,(6分)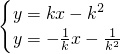 得:
得: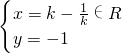
 ,
,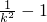 ),
),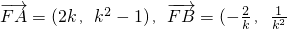 -1),
-1),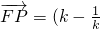 ,-2)
,-2)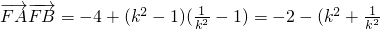 ).
).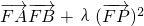 =0.(14分)
=0.(14分)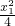 ),由x2=4y,得:y′=
),由x2=4y,得:y′= ,由此推导出直线PA的方程是:y=
,由此推导出直线PA的方程是:y=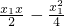 .同理,直线PB的方程是:y=
.同理,直线PB的方程是:y=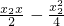 .由此能求出点P的轨迹方程.
.由此能求出点P的轨迹方程.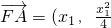 -1),
-1),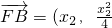 -1),得P(
-1),得P( ,-1)
,-1)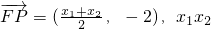 =-4,
=-4,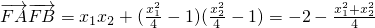 (
(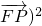 +2,由此能推导出存在λ=1使得
+2,由此能推导出存在λ=1使得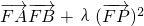 =0.
=0. =0,设PA的直线方程是y=kx+m(k,m∈R,k≠0),由
=0,设PA的直线方程是y=kx+m(k,m∈R,k≠0),由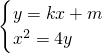 得:x2-4kx-4m=0,△=16k2+16m=0,得到直线PA的方程是:y=kx-k2.同理可得直线PB的方程是:y=-
得:x2-4kx-4m=0,△=16k2+16m=0,得到直线PA的方程是:y=kx-k2.同理可得直线PB的方程是:y=-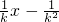 .由此能求出P的轨迹方程.
.由此能求出P的轨迹方程. ,
,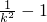 ),知
),知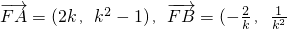 -1),
-1),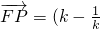 ,-2),由此能推导出存在λ=1使得
,-2),由此能推导出存在λ=1使得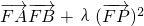 =0.
=0.

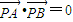 .
.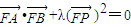 ?若存在,求出λ的值,若不存在,请说明理由.
?若存在,求出λ的值,若不存在,请说明理由.