
分析 随机变量X的所有可能取值为1,2,3,4,根据它们的概率之和为1,求出c的值,进一步求出P(1.5<k<3.5)的值.
解答 解:由随机变量X的分布列为P(X=k)=$\frac{c}{k(k+1)}$(c为常数),k=1,2,3,4,
得$\frac{c}{1×(1+1)}+\frac{c}{2×(2+1)}+\frac{c}{3×(3+1)}$$+\frac{c}{4×(4+1)}=1$,
解c=$\frac{5}{4}$.
∴P(1.5<k<3.5)=P(X=2)+P(X=3)=$\frac{5}{24}+\frac{5}{48}=\frac{5}{16}$.
故答案为:$\frac{5}{16}$.
点评 本题考查了离散型随机变量的期望与方差,解决随机变量的分布列问题,一定要注意分布列的特点,各个概率值在[0,1]之间,概率和为1,属于中档题.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:选择题
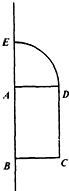 如图所示,矩形ABCD和一个圆心角为90°的扇形拼在一起,其中AB=2,BC=AE=1,则以AB所在直线为旋转轴将整个图形旋转一周所得几何体的表面积为( )
如图所示,矩形ABCD和一个圆心角为90°的扇形拼在一起,其中AB=2,BC=AE=1,则以AB所在直线为旋转轴将整个图形旋转一周所得几何体的表面积为( )| A. | 7π | B. | 5π | C. | 9π | D. | 8π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3\sqrt{5}}{5}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | $\frac{\sqrt{15}}{3}$ | D. | $\frac{\sqrt{21}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 13 | B. | $\sqrt{13}$ | C. | 7 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x1 | 2 | 3 | 4 | 5 | 6 |
| y1 | 2.5 | 4 | 5 | 6 | 7.5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com