
����Ŀ���������ͳ�ƣ�ij��2019���1��1����1��30����30������26�������������.������ͨ���û�����������ָ����AQI����������Ⱦ״�����±���ij����۲���¼������4�������AQIָ��![]() �뵱��Ŀ���ˮƽ�ɼ���
�뵱��Ŀ���ˮƽ�ɼ���![]() �����.
�����.
AQIָ�� | 900 | 700 | 300 | 100 |
����ˮƽ�ɼ��� | 0.5 | 3.5 | 6.5 | 9.5 |
��1����![]() �����ݱ��е����ݣ����
�����ݱ��е����ݣ����![]() ����
����![]() �Ļع鷽�̣�
�Ļع鷽�̣�
��2����ij�����AQTָ��![]() ����ô�������ˮƽ�ɼ��ȴ�ԼΪ���٣�
����ô�������ˮƽ�ɼ��ȴ�ԼΪ���٣�
�����ο����ݣ�![]() ��
��![]() .
.
�ο���ʽ�����Իع�����![]() �У�
��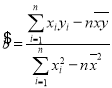 ��
��![]() ������
������![]() Ϊ����ƽ����.
Ϊ����ƽ����.

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() �����Ҷ���Ϊ
�����Ҷ���Ϊ![]() ��
��![]() ����Բ������һ��
����Բ������һ��![]() ������
������![]() ������Բ����
������Բ����![]() .
.
��1������Բ�ı����̣�
��2����![]() �ǹ켣
�ǹ켣![]() �ϵ��������㣬�߶�
�ϵ��������㣬�߶�![]() ���е�
���е�![]() ��ֱ��
��ֱ��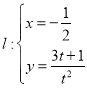 ��Ϊ�������ϣ��߶�
��Ϊ�������ϣ��߶�![]() ���д�����
�������![]() ����
����![]() ���㣬�Ƿ���ڵ�
���㣬�Ƿ���ڵ�![]() ��ʹ��
��ʹ��![]() Ϊֱ����Բ������
Ϊֱ����Բ������![]() �������ڣ����
�������ڣ����![]() �����꣬�������ڣ���˵������.
�����꣬�������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������й������˵����ȷ���ǣ� ��
A.���⡰��![]() ��
��![]() ����
����![]()
![]() 0���ķ�����Ϊ����
0���ķ�����Ϊ����![]() ��
��![]() ����
����![]()
![]() 0��
0��
B.���⡰����f��x������a��1��x��R�ϵ����������ķ��ǡ�����f��x������a��1��x��R�ϵļ�������
C.���⡰����ABC�У���sinA��sinB����A��B�����������Ϊ������
D.���⡰��x��2����x2��3x+2��0����������Ϊ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������![]() �У�
��![]() ����ABCD��
����ABCD��![]() ��
��![]() ��
��![]() ��
��
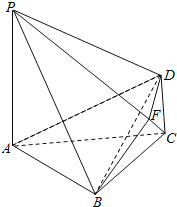
![]() ��
��![]() ��֤��
��֤��![]() ƽ��PAC��
ƽ��PAC��
![]() ��
��![]() ������PC�ϵĵ�F����
������PC�ϵĵ�F����![]() ��������
��������![]() �������
�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���й��ִ�ָ���Ƿ�ӳ�ִ���ҵ��Ӫ�����г���Ҫ��Ʒ����״����仯���Ƶ�����ָ����ϵ����ͼ��ʾ������ͼ��2017���2018����й��ִ�ָ��������������ݸ�����ͼ�����н����в���ȷ���ǣ�������
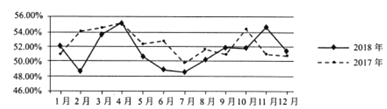
A. 2018��1����4�µIJִ�ָ����2017��ͬ�ڲ����Ը���
B. ����������ִ�ָ����������4�·�
C. 2018��ȫ��ִ�ָ��ƽ��ֵ���Ե���2017��
D. 2018����ִ�ָ������λ����2017����ִ�ָ����λ����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��������ͬ�ļ�ֵ��x1��x2����x1��x2��
��������ͬ�ļ�ֵ��x1��x2����x1��x2��
��1����ʵ��a��ȡֵ��Χ��
��2����֤��x1x2��a2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾Ϊ�˱��Ϊ������Լ��Դ��������һ������������������������͵���Ŀ�����������Ŀ�´����ɱ�![]() ��Ԫ�����´�����
��Ԫ�����´�����![]() ���֣�֮��ĺ�����ϵ���Խ��Ƶر�ʾΪ��
���֣�֮��ĺ�����ϵ���Խ��Ƶر�ʾΪ��
 ����ÿ����һ�������������ɵõ������õ�������ͼ�ֵΪ200Ԫ��������Ŀ�����������������貹����
����ÿ����һ�������������ɵõ������õ�������ͼ�ֵΪ200Ԫ��������Ŀ�����������������貹����
��1����![]() ʱ���жϸ���Ŀ�ܷ������������������������������������������ÿ��������Ҫ��������Ԫ����ʹ����Ŀ������
ʱ���жϸ���Ŀ�ܷ������������������������������������������ÿ��������Ҫ��������Ԫ����ʹ����Ŀ������
��2������Ŀÿ�´�����Ϊ���ٶ�ʱ������ʹÿ�ֵ�ƽ�������ɱ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��![]() ����Բ
����Բ![]() ��,ֱ��
��,ֱ��![]() ��x��y��ֱ���A,B���㣬0Ϊ����ԭ�㣬�ҡ�OAB ���������СֵΪ
��x��y��ֱ���A,B���㣬0Ϊ����ԭ�㣬�ҡ�OAB ���������СֵΪ![]()

(1)����Բ![]() ��������;
��������;
(2) ���C��D��F2�ֱ�Ϊ��Բ![]() ���ϡ��¶����Լ��ҽ��㣬E Ϊ�߶�OD ���е㣬ֱ��F2E ����Բ
���ϡ��¶����Լ��ҽ��㣬E Ϊ�߶�OD ���е㣬ֱ��F2E ����Բ![]() �ཻ��M��N ���㣬��
�ཻ��M��N ���㣬��![]() ������Բ
������Բ![]() �ķ���.
�ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ϵ![]() �У�����
�У�����![]() ��x�ύ��A��B���㣬��Q������Ϊ
��x�ύ��A��B���㣬��Q������Ϊ![]() .
.
��1���Ƿ����b��ʹ��![]() ������������bֵ����������ڣ�˵�����ɣ�
������������bֵ����������ڣ�˵�����ɣ�
��2����A��B��Q�����Բ�����Сʱ����Բ�ķ���.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com