
| 1 | 2 |
 解:由题意,将△PCD沿CD折起后,PA⊥平面ABCD.四边形ABCD是边长为2的正方形,PD=2.
解:由题意,将△PCD沿CD折起后,PA⊥平面ABCD.四边形ABCD是边长为2的正方形,PD=2.| DF |
| DG |
| EF |
| EG |
| |m•n| |
| |m||n| |
| ||
| 5 |


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:高中数学 来源: 题型:
| 6 |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年浙江省宁波市五校高三适应性考试文科数学试卷(解析版) 题型:解答题
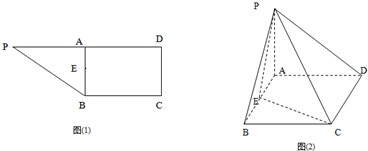
如图(1)在直角梯形ABCD中,AB//CD,AB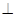 AD且AB=AD=
AD且AB=AD=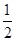 CD=1,现以AD为一边向梯形外作正方形ADEF,然后沿AD将正方形翻拆,使平面ADEF与平面ABCD互相垂直如图(2)。
CD=1,现以AD为一边向梯形外作正方形ADEF,然后沿AD将正方形翻拆,使平面ADEF与平面ABCD互相垂直如图(2)。

(1)求证平面BDE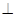 平面BEC
平面BEC
(2)求直线BD与平面BEF所成角的正弦值。
查看答案和解析>>
科目:高中数学 来源:2010年普通高等学校招生全国统一考试(重庆卷)数学理工类模拟试卷(一) 题型:解答题
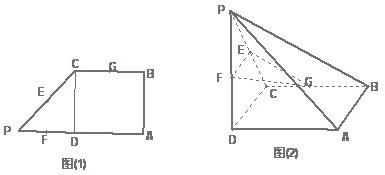
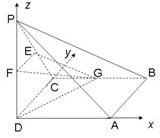
如图(1)在直角梯形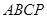 中,
中,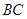 ∥
∥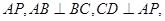
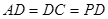 =2,
=2, 、
、 、
、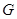 分别是
分别是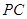 、
、 、
、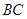 的中点,现将
的中点,现将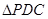 沿
沿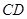 折起,使平面
折起,使平面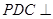 平面
平面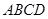 (如图2).
(如图2).
(Ⅰ)求二面角 的大小;
的大小;
(Ⅱ)在线段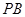 上确定一点
上确定一点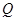 ,使
,使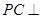 平面
平面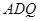 ,并给出证明过程.
,并给出证明过程.
 |
查看答案和解析>>
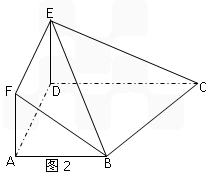
科目:高中数学 来源:浙江省模拟题 题型:解答题
 CD=1,现以AD为一边向梯形外作正方形ADEF,然后沿AD将正方形翻拆,使平面ADEF与平面ABCD互相垂直如图(2)。
CD=1,现以AD为一边向梯形外作正方形ADEF,然后沿AD将正方形翻拆,使平面ADEF与平面ABCD互相垂直如图(2)。 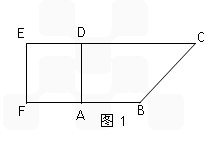
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com