
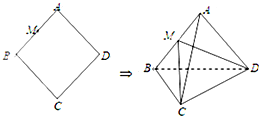
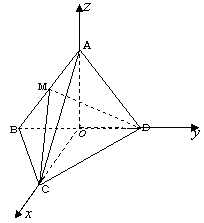
 在边长为5的菱形ABCD中,AC=8,现沿对角线BD把△ABD折起,折起后使∠ADC的余弦值为
在边长为5的菱形ABCD中,AC=8,现沿对角线BD把△ABD折起,折起后使∠ADC的余弦值为| 9 |
| 25 |
| 9 |
| 25 |
| 3 |
| 2 |
| MC |
| 3 |
| 2 |
| AC |
| DC |
| n |
|
|
| n |
| MA |
| 3 |
| 2 |
|
| ||||
|
|
| |0+6+6| | ||
|
6
| ||
| 17 |
| 1 |
| 2 |
| 25-16 |
| 1 |
| 3 |
| 1 |
| 3 |
6
| ||
| 17 |
24
| ||
| 17 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
| A、0 | B、1 | C、2 | D、3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
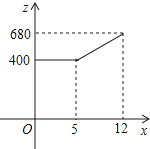 我市某服装厂生产的服装供不应求,A车间接到生产一批西服的紧急任务,要求必须在12天内完成.为了加快进度,车间采取工人分批日夜加班,机器满负荷运转的生产方式,生产效率得到了提高,每天生产的西服数量y(套)与时间x(天)的关系如下表:
我市某服装厂生产的服装供不应求,A车间接到生产一批西服的紧急任务,要求必须在12天内完成.为了加快进度,车间采取工人分批日夜加班,机器满负荷运转的生产方式,生产效率得到了提高,每天生产的西服数量y(套)与时间x(天)的关系如下表:| 时间x(天) | 1 | 2 | 3 | 4 | … |
| 每天产量y(套) | 22 | 24 | 26 | 28 | … |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com