
分析 f(x)=$\left\{\begin{array}{l}{2-2x\\;\\;\frac{3}{4}≤x<1}\\{2x-1\\;\\;\frac{1}{2}≤x<\frac{3}{4}}\end{array}\right.$,此时f(x)∈[0,$\frac{1}{2}$],∵f(2x)=2f(x),∴x∈[1,2)时,f(x)∈[0,1],∴x∈[2,4)时,f(x)∈[0,2],…以此类推,
则F(x)=f(x)-a在区间(1,2)有2个零点,分别为x1,x2,且满足x1+x2=2×$\frac{3}{2}$=3,
依此类推:x3+x4=6,…,x2n-1+x2n=3×2n-1.利用等比数列的前n项和公式即可得出.
解答 解:f(x)=$\left\{\begin{array}{l}{2-2x\\;\\;\frac{3}{4}≤x<1}\\{2x-1\\;\\;\frac{1}{2}≤x<\frac{3}{4}}\end{array}\right.$,此时f(x)∈[0,$\frac{1}{2}$],
∵f(2x)=2f(x),∴x∈[1,2)时,f(x)∈[0,1],∴x∈[2,4)时,f(x)∈[0,2],…以此类推,
则F(x)=f(x)-a在区间(1,2)有2个零点,分别为x1,x2,且满足x1+x2=2×$\frac{3}{2}$=3,
依此类推:x3+x4=6,…,x2n-1+x2n=3×2n-1.如图所示: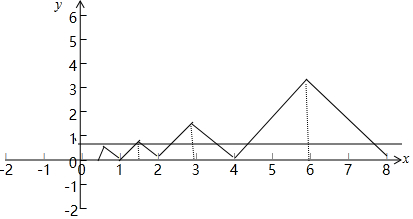
则x1+x2+…+x2n-1+x2n=3×(2n-1).
故答案为:3×(2n-1).
点评 本题考查了函数的图象与性质、区间转换、对称性、等比数列的前n项和公式等基础知识与基本技能,属于难题


科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{37}$-6 | B. | 10-3$\sqrt{5}$ | C. | 8-$\sqrt{37}$ | D. | 2$\sqrt{5}$-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 31 | C. | -33 | D. | -31 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
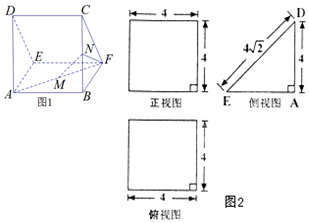 一个多面体的直观图(图1)及三视图(图2)如图所示,其中M、N分别是AF、BC的中点,
一个多面体的直观图(图1)及三视图(图2)如图所示,其中M、N分别是AF、BC的中点,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\frac{25}{3}$或 3 | C. | $\sqrt{5}$ | D. | $\frac{{5\sqrt{15}}}{3}$或$\sqrt{15}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | $\frac{15}{2}$ | D. | $\frac{17}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
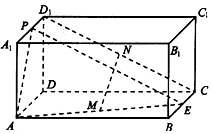 如图,在长方体ABCD-A1B1C1D1中,E、P分别是BC、A1D1的中点.M、N分别是AE、CD1的中点,AD=AA1=$\frac{1}{2}$AB=2.
如图,在长方体ABCD-A1B1C1D1中,E、P分别是BC、A1D1的中点.M、N分别是AE、CD1的中点,AD=AA1=$\frac{1}{2}$AB=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com