Question

【题目】某家电公司销售部门共有200位销售员，每位部门对每位销售员都有1400万元的年度销售任务，已知这200位销售员去年完成销售额都在区间（单位：百万元）内，现将其分成5组，第1组，第2组，第3组，第4组，第5组对应的区间分别为， ， ， ， ，绘制出频率分布直方图.

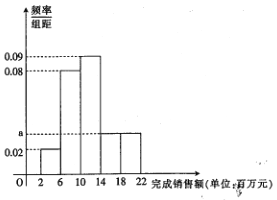
（1）求的值，并计算完成年度任务的人数；

（2）用分层抽样从这200位销售员中抽取容量为25的样本，求这5组分别应抽取的人数；

（3）现从（2）中完成年度任务的销售员中随机选取2位，奖励海南三亚三日游，求获得此奖励的2位销售员在同一组的概率.

Answer 1

【答案】（Ⅰ）,;（Ⅱ）见解析;　（Ⅲ）．

【解析】试题分析：（1）频率分布直方图中所有小长方形面积之和为1,所以有，解得的值，根据小长方形面积对应区间概率,以及频数等于总数与频率乘积得完成年度任务的人数为.（2）分成抽样就是按比例,可按小长方形纵坐标之比进行分人数,（3）完成年度任务的销售员中共有6人,利用枚举法得6人中随机选取2位，所有的基本事件数为15,其中在同一组基本事件数有6个，最后根据古典概型概率公式计算概率.

试题解析：（Ⅰ）∵，∴．　

完成年度任务的人数为.

（Ⅱ）第1组应抽取的人数为，

第2组应抽取的人数为，

第3组应抽取的人数为，

第4组应抽取的人数为，

第5组应抽取的人数为．　

（Ⅲ）在（Ⅱ）中完成年度任务的销售员中，第4组有3人，记这3人分别为， ， ，第5组有3人，记这3人分别为， ， ．　

从这6人中随机选取2位，所有的基本事件为： ， ， ， ， ， ， ， ， ， ， ， ， ， ， ，共有15个基本事件．

获得此奖励的2位销售员在同一组的基本事件有6个，

故所求概率为．