
【题目】某租赁公司拥有汽车100辆.当每辆车的月租金为3000元时,可全部租出,当每辆车的月租金每增加50元时,未租出的车将会增加一辆,租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.,当每辆车的月租金定为x元时,租赁公司的月收益为y元,
(1)试写出x,y的函数关系式(不要求写出定义域);
(2)租赁公司某月租出了88辆车,求租赁公司的月收益多少元?
【答案】
(1)解:设每辆车的月租金定为x元,则租赁公司的月收益为:
y=(100﹣ ![]() )(x﹣150)﹣
)(x﹣150)﹣ ![]() ×50,
×50,
整理得:y=﹣ ![]() x2+162x﹣21000
x2+162x﹣21000
(2)解:租赁公司某月租出了88辆车,
每辆车的月租金为3000+50×12=3600元,
当x=3600时,y=﹣ ![]() ×36002+162×3600﹣21000=303000元
×36002+162×3600﹣21000=303000元
当租出了88辆车时,租赁公司的月收益303000元
【解析】(1)设每辆车的月租金定为x元,则租赁公司的月收益为:y=(100﹣ ![]() )(x﹣150)﹣
)(x﹣150)﹣ ![]() ×50,整理可得答案;(2)租赁公司某月租出了88辆车,每辆车的月租金为3000+50×2=3600元,代入(1)中解析式,可得答案.
×50,整理可得答案;(2)租赁公司某月租出了88辆车,每辆车的月租金为3000+50×2=3600元,代入(1)中解析式,可得答案.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】为响应国家“精准扶贫,产业扶贫”的战略,某市面向全市征召《扶贫政策》义务宣传志愿者,从年龄在![]() 的500名志愿者中随机抽取100名,其年龄频率分布直方图如图所示.
的500名志愿者中随机抽取100名,其年龄频率分布直方图如图所示.
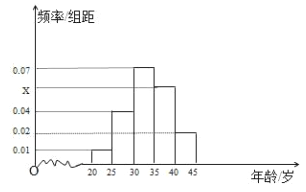
(Ⅰ)求图中![]() 的值;
的值;
(Ⅱ)在抽出的100名志愿者中按年龄采用分层抽样的方法抽取10名参加中心广场的宣传活动,再从这10名志愿者中选取3名担任主要负责人.记这3名志愿者中“年龄低于35岁”的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“杨辉三角”又称“贾宪三角”,是因为贾宪约在公元1050年首先使用“贾宪三角”进行高次开方运算,而杨辉在公元1261年所著的《详解九章算法》一书中,记录了贾宪三角形数表,并称之为“开方作法本源”图.下列数表的构造思路就源于“杨辉三角”.该表由若干行数字组成,从第二行起,每一行中的数字均等于其“肩上”两数之和,表中最后一行仅有一个数,则这个数是( )
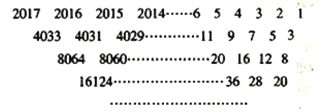
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() 的定义域为集合A,函数g(x)=(
的定义域为集合A,函数g(x)=( ![]() )x(﹣1≤x≤0)的值域为集合B.
)x(﹣1≤x≤0)的值域为集合B.
(1)求A∩B;
(2)若集合C=[a,2a﹣1],且C∪B=B,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】六个面都是平行四边形的四棱柱称为平行六面体.已知在平行四边形ABCD中(如图1),有AC2+BD2=2(AB2+AD2),则在平行六面体ABCD﹣A1B1C1D1中(如图2),AC12+BD12+CA12+DB12等于( ) 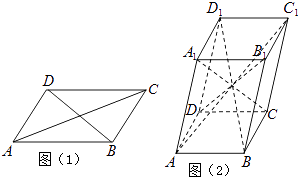
A.2(AB2+AD2+AA12)
B.3(AB2+AD2+AA12)
C.4(AB2+AD2+AA12)
D.4(AB2+AD2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lg(ax﹣bx)(a>1>b>0).
(1)求f(x)的定义域;
(2)若f(x)在(1,+∞)上递增且恒取正值,求a,b满足的关系式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某产品生产厂家生产一种产品,每生产这种产品x(百台),其总成本为G(x)(万元),其中固定成本为42万元,且每生产1百台的生产成本为15万元(总成本=固定成本+生产成本).销售收入R(x)(万元)满足 ![]() 假定该产品产销平衡(即生产的产品都能卖掉),根据上述规律,完成下列问题:
假定该产品产销平衡(即生产的产品都能卖掉),根据上述规律,完成下列问题:
(1)写出利润函数y=f(x)的解析式(利润=销售收入﹣总成本);
(2)要使工厂有盈利,求产量x的范围;
(3)工厂生产多少台产品时,可使盈利最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,离心率为
,离心率为![]() ,两焦点分别为
,两焦点分别为![]() ,过
,过![]() 的直线交椭圆
的直线交椭圆![]() 于
于![]() 两点,且
两点,且![]() 的周长为8.
的周长为8.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作圆
作圆![]() 的切线
的切线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,求弦长
两点,求弦长![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com