已知函数
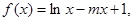
其中
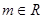
,
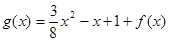
.
(1)若
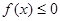
在
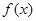
的定义域内恒成立,则实数
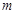
的取值范围
;
(2)在(1)的条件下,当
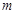
取最小值时,
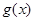
在
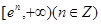
上有零点,则
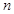
的最大值为
.
(1)
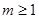
;(2)-2.
试题分析:(1)易知函数
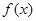
的定义域为
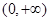
,
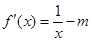
.当
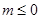
时,在定义域
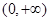
上,
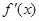
恒大于0.即函数
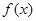
在定义域
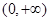
上是增函数,因为
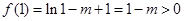
,故
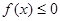
在
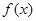
的定义域内不能恒成立;当
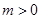
时,在
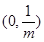
上,
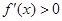
.在
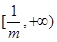
上,
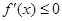
.即函数
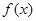
在
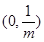
上是增函数,在
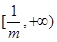
上是减函数.所以
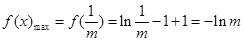
.
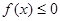
在
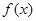
的定义域内恒成立,则
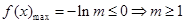
.
(2)由(1)得
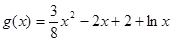
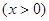
, 所以
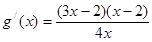
.
故
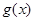
在
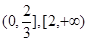
上递增,在
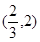
上递减. 所以在
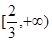
上
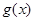
的最小值为
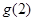
,
而
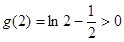
,故
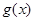
在
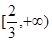
上没有零点. 所以
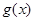
的零点一定在递增区间
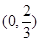
上,从而有
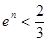
且
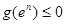
. 又
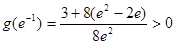
,
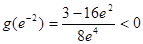
,当
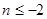
时均有
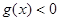
,所以
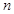
的最大值为-2.
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
若非零函数
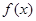
对任意实数
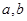
均有
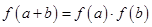
,且当
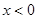
时,
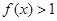
.
(1)求证:
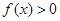
(2)求证:
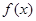
为减函数;
(3)当
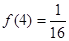
时,解不等式
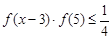
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知函数
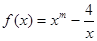
的图象过点(2,0).
⑴求m的值;
⑵证明
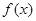
的奇偶性;
⑶判断
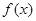
在
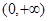
上的单调性,并给予证明;
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已函数
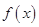
是定义在
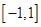
上的奇函数,在
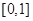
上时
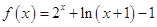
(Ⅰ)求函数
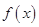
的解析式;
(Ⅱ)解不等式
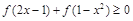
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
定义在
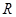
上的函数
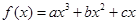
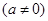
的单调增区间为
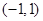
,若方程
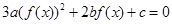
恰有4个不同的实根,则实数
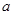
的值为( )
A.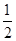 | B.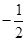 | C.1 | D.-1 |
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
偶函数
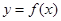
在区间[0,4]上单调递减,则有( )
查看答案和解析>>

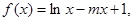 其中
其中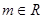 ,
,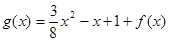 .
.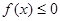 在
在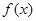 的定义域内恒成立,则实数
的定义域内恒成立,则实数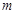 的取值范围 ;
的取值范围 ;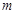 取最小值时,
取最小值时,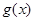 在
在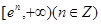 上有零点,则
上有零点,则 的最大值为 .
的最大值为 . 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案