
分析 推导出$\left\{{\begin{array}{l}{m-4=λ}\\{2+6=-2λ}\end{array}}\right.$,由此能求出结果.
解答 解:∵矩阵M=$|\begin{array}{l}{m}&{2}\\{2}&{-3}\end{array}|$的一个特征值λ对应的特征向量为$[\begin{array}{l}{1}\\{-2}\end{array}]$,
∴$\left\{{\begin{array}{l}{m-4=λ}\\{2+6=-2λ}\end{array}}\right.$,…(8分)
解得m=0,λ=-4.…(10分)
点评 本题考查实数值的求法,是基础题,解题时要认真审题,注意特征向量的性质的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | -5 | D. | -4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{5}{2}$ | C. | 3 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向右平移$\frac{2π}{9}$个单位 | B. | 向左平移$\frac{2π}{9}$个单位 | ||
| C. | 向右平移$\frac{2π}{3}$个单位 | D. | 向左平移$\frac{2π}{3}$个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
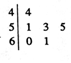 为了检查某高三毕业班学生的体重情况,从该班随机抽取了6位学生进行称重,如图为6位学生体重的茎叶图(单位:kg),其中图中左边是体重的十位数字,右边是个位数字,则这6位学生体重的平均数为( )
为了检查某高三毕业班学生的体重情况,从该班随机抽取了6位学生进行称重,如图为6位学生体重的茎叶图(单位:kg),其中图中左边是体重的十位数字,右边是个位数字,则这6位学生体重的平均数为( )| A. | 52 | B. | 53 | C. | 54 | D. | 55 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com