解:(I)直线l化成斜截式y=-

x-

,再令x=-1,得y=-1,
可得直线l为经过点M(-1,-1),斜率为-

的直线
∴直线l上一点P坐标可写成P(-1+2t,-1-t)
可得直线l的参数方程为
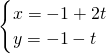
,(t为参数),…(2分)
对于曲线C:ρ
2-2

ρsin(θ+45°)-7=0,即ρ
2-2(ρsinθ+ρcosθ)-7=0.
∵ρ
2=x
2+y
2,ρsinθ=y,ρcosθ=x,
∴曲线C的直角坐标方程为:x
2+y
2-2x-2y-7=0,化成标准方程为(x-1)
2+(y-1)
2=9
得曲线C是以(1,1)为圆半径为3的圆,因此令x-1=3cosθ,y-1=3sinθ
曲线C的参数方程为:

(θ为参数) …(5分)
(II)直线l的普通方程为x+2y+3=0,…①
曲线C普通方程为(x-1)
2+(y-1)
2=9,…②
联解得,
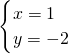
或
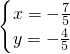
∴直线l和曲线C交点的直角坐标为A(1,-2),B(-

,-

) …(10分)
分析:(I)将直线l化成斜截式,得到它的斜率,再取直线上点M(-1,-1),可得直线l上一点P坐标的参数形式,即可化为直线l的参数方程;对于曲线C,先将其化为直角坐标方程,得到它是以(1,1)为圆半径为3的圆,由此不难得到曲线C的参数方程;
(II)由(I)的结论,将直线l和曲线C的直角坐标方程组成方程组,联解即得方程组的解,即为直线l和曲线C交点的直角坐标.
点评:本题以直线与圆的位置关系作为载体,考查了直线的参数方程、圆的极坐标方程与普通方程的互化等知识,属于基础题.

 ρsin(θ+45°)-7=0.
ρsin(θ+45°)-7=0. x-
x- ,再令x=-1,得y=-1,
,再令x=-1,得y=-1, 的直线
的直线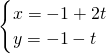 ,(t为参数),…(2分)
,(t为参数),…(2分) ρsin(θ+45°)-7=0,即ρ2-2(ρsinθ+ρcosθ)-7=0.
ρsin(θ+45°)-7=0,即ρ2-2(ρsinθ+ρcosθ)-7=0. (θ为参数) …(5分)
(θ为参数) …(5分)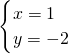 或
或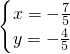
 ,-
,- ) …(10分)
) …(10分)

 A.选修4-1:几何证明选讲
A.选修4-1:几何证明选讲