
【题目】下列判断正确的是( )
A.线性回归直线![]() 必经过点
必经过点![]() ,
,![]() ,…
,…![]() 中心点
中心点![]()
B.从独立性检验可知有99%的把握认为吃地沟油与患胃肠癌有关系时,我们就说如果某人吃地沟油,那么他有99%可能患胃肠癌
C.若两个随机变量的线性相关性越强,则相关系数![]() 的绝对值越接近于1
的绝对值越接近于1
D.将一组数据的每一个数据都加上或减去同一个常数后,其方差也要加上或减去这个常数
科目:高中数学 来源: 题型:
【题目】在疫情这一特殊时期,教育行政部门部署了“停课不停学”的行动,全力帮助学生在线学习.复课后进行了摸底考试,某校数学教师为了调查高三学生这次摸底考试的数学成绩与在线学习数学时长之间的相关关系,对在校高三学生随机抽取45名进行调查.知道其中有25人每天在线学习数学的时长是不超过1小时的,得到了如下的等高条形图:
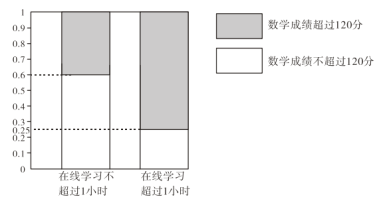
(Ⅰ)是否有![]() 的把握认为“高三学生的这次摸底考试数学成绩与其在线学习时长有关”;
的把握认为“高三学生的这次摸底考试数学成绩与其在线学习时长有关”;
(Ⅱ)将频率视为概率,从全校高三学生这次数学成绩超过120分的学生中随机抽取10人,求抽取的10人中每天在线学习时长超过1小时的人数的数学期望和方差.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
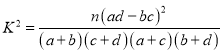
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某媒体对“男女延迟退休”这一公众关注的问题进行了民意调查,下表是在某单位调查后得到的数据(人数):
赞同 | 反对 | 合计 | |
男 | 5 | 6 | 11 |
女 | 11 | 3 | 14 |
合计 | 16 | 9 | 25 |
(1)能否有90%以上的把握认为对这一问题的看法与性别有关?
(2)进一步调查:
①从赞同“男女延迟退休”的![]() 人中选出
人中选出![]() 人进行陈述发言,求事件“男士和女士各至少有
人进行陈述发言,求事件“男士和女士各至少有![]() 人发言”的概率;
人发言”的概率;
②从反对“男女延迟退休”的![]() 人中选出
人中选出![]() 人进行座谈,设选出的
人进行座谈,设选出的![]() 人中女士人数为
人中女士人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
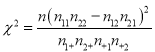
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】焦点在x轴上的椭圆C:![]() 经过点
经过点![]() ,椭圆C的离心率为
,椭圆C的离心率为![]() .
.![]() ,
,![]() 是椭圆的左、右焦点,P为椭圆上任意点.
是椭圆的左、右焦点,P为椭圆上任意点.
(1)求椭圆的标准方程;
(2)若点M为![]() 的中点(O为坐标原点),过M且平行于OP的直线l交椭圆C于A,B两点,是否存在实数
的中点(O为坐标原点),过M且平行于OP的直线l交椭圆C于A,B两点,是否存在实数![]() ,使得
,使得![]() ;若存在,请求出
;若存在,请求出![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某品牌经销商在一广场随机采访男性和女性用户各50名,其中每天玩微信超过6小时的用户列为“微信控”,否则称其为“非微信控”,调查结果如下:
微信控 | 非微信控 | 合计 | |
男性 | 26 | 24 | 50 |
女性 | 30 | 20 | 50 |
合计 | 56 | 44 | 100 |
(1)根据以上数据,能否有95%的把握认为“微信控”与“性别”有关?
(2)现从调查的女性用户中按分层抽样的方法选出5人,求所抽取的5人中“微信控”和“非微信控”的人数;
(3)从(2)中抽取的5位女性中,再随机抽取3人赠送礼品,试求抽取3人中恰有2人位“微信控”的概率.
参考公式: 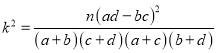 ,其中
,其中![]() .
.
参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了鼓励市民节约用电,实行“阶梯式”电价,将该市每户居民的月用电量划分为三档,月用电量不超过200度的部分按![]() 元/度收费,超过200度但不超过400度的部分按
元/度收费,超过200度但不超过400度的部分按![]() 元/度收费,超过400度的部分按1.0元/度收费.
元/度收费,超过400度的部分按1.0元/度收费.

(Ⅰ)求某户居民用电费用![]() (单位:元)关于月用电量
(单位:元)关于月用电量![]() (单位:度)的函数解析式;
(单位:度)的函数解析式;
(Ⅱ)为了了解居民的用电情况,通过抽样,获得了今年1月份100户居民每户的用电量,统计分析后得到如图所示的频率分布直方图,若这100户居民中,今年1月份用电费用不超过260元的占![]() ,求
,求![]() ,
, ![]() 的值;
的值;
(Ⅲ)在满足(Ⅱ)的条件下,若以这100户居民用电量的频率代替该月全市居民用户用电量的概率,且同组中的数据用该组区间的中点代替,记![]() 为该居民用户1月份的用电费用,求
为该居民用户1月份的用电费用,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地政府为科技兴市,欲将如图所示的一块不规则的非农业用地![]() 规划建成一个矩形的高科技工业园区.已知
规划建成一个矩形的高科技工业园区.已知![]() ,
,![]() ,
,![]() ,曲线段
,曲线段![]() 是以点
是以点![]() 为顶点且开口向上的抛物线的一段.如果要使矩形的相邻两边分别落在
为顶点且开口向上的抛物线的一段.如果要使矩形的相邻两边分别落在![]() 、
、![]() 上,且一个顶点
上,且一个顶点![]() 落在曲线段
落在曲线段![]() 上,问应如何规划才能使矩形工业园区的用地面积最大?并求出最大的用地面积(精确到
上,问应如何规划才能使矩形工业园区的用地面积最大?并求出最大的用地面积(精确到![]() ).
).

查看答案和解析>>
科目:高中数学 来源: 题型:
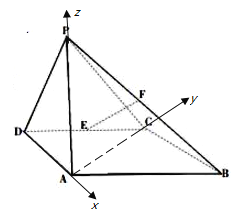
【题目】如图所示,四棱锥![]() 中,侧面
中,侧面![]() 底面
底面![]() ,底面
,底面![]() 是平行四边形,
是平行四边形,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 中点,点
中点,点![]() 在线段
在线段![]() 上.
上.
(Ⅰ)证明:![]() ;
;
(Ⅱ)若![]()
![]()
![]()
![]() ,求实数
,求实数![]() 使直线
使直线![]() 与平面
与平面![]() 所成角和直线
所成角和直线![]() 与平面
与平面![]() 所成角相等.
所成角相等.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com