
分析 (Ⅰ)先求导函数,通过讨论a,直接让导函数大于0求出增区间,导函数小于0求出减区间即可;
(Ⅱ)直接利用切线的斜率即为切点处的导数值以及切点是直线与曲线的共同点联立方程即可求实数a的值;
(Ⅲ)先求出g(x)的导函数,分情况讨论出函数在区间[1,e]上的单调性,进而求得其在区间[1,e]上的最小值.
解答 解:(Ⅰ)因为函数f(x)=$\frac{a(x-1)}{{x}^{2}}$,
∴f′(x)=$\frac{a(2-x)}{{x}^{3}}$,
a>0时,f′(x)>0⇒0<x<2,f′(x)<0⇒x<0,或x>2,
故函数f(x)的单调增区间为(0,2),单调减区间为(-∞,0)和(2,+∞),
a<0时,f′(x)<0⇒0<x<2,f′(x)>0⇒x<0,或x>2,
故函数f(x)的单调减区间为(0,2),单调增区间为(-∞,0)和(2,+∞),
(Ⅱ)设切点为(x,y),
由切线斜率k=1=$\frac{a(2-x)}{{x}^{3}}$,⇒x3=-ax+2a,①
由x-y-1=x-$\frac{a(x-1)}{{x}^{2}}$-1=0⇒(x2-a)(x-1)=0⇒x=1,x=±$\sqrt{a}$.
把x=1代入①得a=1,
把x=$\sqrt{a}$代入①得a=1,
把x=-$\sqrt{a}$代入①得a=-1(舍去),
故所求实数a的值为1.
(Ⅲ)∵g(x)=xlnx-x2f(x)=xlnx-a(x-1),
∴g′(x)=lnx+1-a,解lnx+1-a=0得x=ea-1,
故g(x)在区间(ea-1,+∞)上递增,在区间(0,ea-1)上递减,
①当ea-1≤1时,即0<a≤1时,g(x)在区间[1,e]上递增,其最小值为g(1)=0;
②当1<ea-1<e时,即1<a<2时,g(x)的最小值为g(ea-1)=a-ea-1;
③当ea-1≥e,即a≥2时,g(x)在区间[1,e]上递减,其最小值为g(e)=e+a-ae.
点评 本题主要考查利用导数求闭区间上函数的最值以及利用导数研究函数的单调性,是高考的常考题型.


科目:高中数学 来源:2015-2016学年江西省南昌市高二理下学期期末考试数学试卷(解析版) 题型:解答题
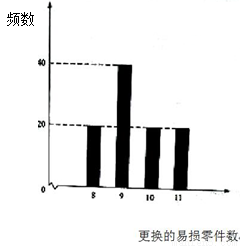
某公司计划购买2台机器,该种机器使用三年后即被淘汰.机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个200元.在机器使用期间,如果备件不足再购买,则每个500元.现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数,得下面柱状图:
以这100台机器更换的易损零件数的频率代替1台机器更换的易损零件数发生的概率,记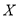 表示2台机器三年内共需更换的易损零件数,
表示2台机器三年内共需更换的易损零件数,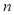 表示购买2台机器的同时购买的易损零件数.
表示购买2台机器的同时购买的易损零件数.
(I)求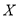 的分布列;
的分布列;
(II)若要求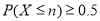 ,确定
,确定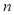 的最小值;
的最小值;
(III)以购买易损零件所需费用的期望值为决策依据,在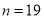 与
与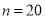 之中选其一,应选用哪个?
之中选其一,应选用哪个?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
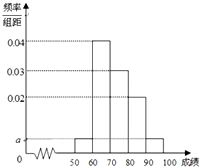 某校100名学生期末考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].
某校100名学生期末考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,在透明塑料制成的长方体ABCD-A1B1C1D1容器内灌进一些水,将容器底面一边BC固定于地面上,再将容器倾斜,随着倾斜度的不同,有下列四个说法:
如图,在透明塑料制成的长方体ABCD-A1B1C1D1容器内灌进一些水,将容器底面一边BC固定于地面上,再将容器倾斜,随着倾斜度的不同,有下列四个说法:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{2}$+$\frac{{y}^{2}}{3}$=1 | B. | 2x2+3y2=1 | C. | $\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{9}$=1 | D. | 4x2+9y2=1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com