
【题目】为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样的方法从该地区调查了500位老年人,结果如下:
性别 是否需要志愿者 | 男 | 女 |
需要 | 40 | 30 |
不需要 | 160 | 270 |
附:![]() 的观测值
的观测值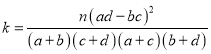
| 0.05 | 0.01 | 0.001 |
| 3.841 | 6.635 | 10.828 |
(1)估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
(2)在犯错误的概率不超过0.01的前提下是否可认为该地区的老年人是否需要志愿者提供帮助与性别有关?
 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:
【题目】如图所示,三国时代数学家赵爽在《周髀算经》中利用弦图,给出了勾股定理的绝妙证明.图中包含四个全等的直角三角形及一个小正方形(阴影),设直角三角形有一内角为![]() ,若向弦图内随机抛掷500颗米粒(大小忽略不计,取
,若向弦图内随机抛掷500颗米粒(大小忽略不计,取![]() ),则落在小正方形(阴影)内的米粒数大约为( )
),则落在小正方形(阴影)内的米粒数大约为( )
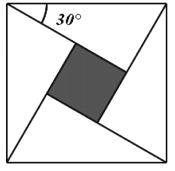
A. 134 B. 67 C. 200 D. 250
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年8月教育部、国家卫生健康委员会等八个部门联合印发《综合防控儿童青少年近视实话方案》中明确要求,为切实加强新时代儿童青少年近视防控工作,学校应严格组织全体学生每天上、下午各大做1次眼保健操.为了了解学校推广眼保健操是否能有效预防近视,随机从甲学校抽取了50名学生,再从乙学校选出与甲学校被抽取的50名学生视力情况一样的50学生(期中甲学校每天安排学生做眼保健操,乙学校不安排做跟保健操),一段时间后检测他们的视力情况并统计,若视力情况为1.0及以上,则认为该学生视力良好,否则认为该学生的视力一般,表1为甲学校视力情况的频率分布表,表2为乙学校学生视力情况的频率分布表,根据表格回答下列问题:
表1 甲学校学生视力情况的频率分布表
视力情况 | 0.6 | 0.8 | 1.0 | 1.2 | 1.5 |
频 数 | 1 | 1 | 15 | 15 | 18 |
表2 乙学校学生视力情况的频率分布表
视力情况 | 0.5 | 0.6 | 0.8 | 1.0 | 1.2 | 1.5 |
频 数 | 2 | 2 | 4 | 19 | 13 | 10 |
(1)求在甲学校的50名学生中随机选择1名同学,求其视力情况为良好的概率;
(2)根据表1,表2,对在学校推广眼保健操的必要性进行分析;
(3)在乙学校视力情况一般的学生中选择2人,了解其具体用眼习惯,求这两人视力情况都为0.8的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】酒驾是严重危害交通安全的违法行为.为了保障交通安全,根据国家有关规定:100mL血液中酒精含量低于20mg的驾驶员可以驾驶汽车,酒精含量达到20~79mg的驾驶员即为酒后驾车,80mg及以上认定为醉酒驾车.假设某驾驶员喝了一定量的酒后,其血液中的酒精含量上升到了1mg/mL.如果在停止喝酒以后,他血液中酒精含量会以每小时30%的速度减少,那么他至少经过几个小时才能驾驶汽车?( )(参考数据:lg0.2≈﹣0.7,1g0.3≈﹣0.5,1g0.7≈﹣0.15,1g0.8≈﹣0.1)
A.1B.3C.5D.7
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在底面边长为![]() 、高为
、高为![]() 的正六棱柱
的正六棱柱![]() 展厅内,长为
展厅内,长为![]() ,宽为
,宽为![]() 的矩形油画
的矩形油画![]() 挂在厅内正前方中间.
挂在厅内正前方中间.
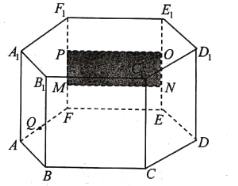
(1)求证:平面![]() 平面
平面![]() ;
;
(2)当游客![]() 在
在![]() 上看油画的纵向视角(即
上看油画的纵向视角(即![]() )最大时,求
)最大时,求![]() 与油画平面所成的角.
与油画平面所成的角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 的展开式中各项系数的和为2,则下列结论正确的有( )
的展开式中各项系数的和为2,则下列结论正确的有( )
A.![]()
B.展开式中常数项为160
C.展开式系数的绝对值的和1458
D.若![]() 为偶数,则展开式中
为偶数,则展开式中![]() 和
和![]() 的系数相等
的系数相等
查看答案和解析>>
科目:高中数学 来源: 题型:
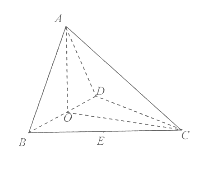
【题目】如图,四面体ABCD中,O、E分别是BD、BC的中点,![]() ,
,![]() .
.
(1)求证:![]() 平面BCD;
平面BCD;
(2)求异面直线AB与CD所成角的余弦值;
(3)求点E到平面ACD的距离。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车站在春运期间为了了解旅客购票情况,随机抽样调查了100名旅客从开始在售票窗口排队到购到车票所用的时间t(以下简称为购票用时,单位为min),下面是这次调查统计分析得到的频率分布表和频率分布直方图(如图所示).
分组 | 频数 | 频率 | |
一组 | 0≤t<5 | 0 | 0 |
二组 | 5≤t<10 | 10 | 0.10 |
三组 | 10≤t<15 | 10 | ② |
四组 | 15≤t<20 | ① | 0.50 |
五组 | 20≤t≤25 | 30 | 0.30 |
合计 | 100 | 1.00 |

解答下列问题:
(1)这次抽样的样本容量是多少?
(2)在表中填写出缺失的数据并补全频率分布直方图;
(3)旅客购票用时的平均数可能落在哪一组?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com