设圆(x-3)2+(y+5)2=r2(r>0)上有且仅有两个点到直线4x-3y-2=0的距离等于1,则圆半径r的取值范围是 .
【答案】
分析:先根据圆的方程求得圆心坐标和圆心到已知直线的距离,进而可推断出与直线4x-3y-2=0距离是1的两个直线方程,分别求得圆心到这两直线的距离,分析如果与4x-3y+3=0相交 那么圆也肯定与4x-3y-7=0相交 交点个数多于两个,则到直线4x-3y-2=0的距离等于1的点不止2个,进而推断出圆与4x-3y+3=0不相交;同时如果圆与4x-3y-7=0的距离小于等于1 那么圆与4x-3y-7=0和4x-3y+3=0交点个数和至多为1个 也不符合题意,最后综合可知圆只能与4x-3y-7=0相交,与4x-3y+3=0相离,进而求得半径r的范围.
解答:解:依题意可知圆心坐标为(3,-5),到直线的距离是5
与直线4x-3y-2=0距离是1的直线有两个4x-3y-7=0和4x-3y+3=0
圆心到4x-3y-7=0距离为
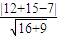
=4 到4x-3y+3=0距离是
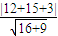
=6
如果圆与4x-3y+3=0相交 那么圆也肯定与4x-3y-7=0相交,
交点个数多于两个,于是圆上点到4x-3y-2=0的距离等于1的点不止两个
所以圆与4x-3y+3=0不相交
如果圆与4x-3y-7=0的距离小于等于1,那么圆与4x-3y-7=0和4x-3y+3=0交点个数和至多为1个
所以圆只能与4x-3y-7=0相交,与4x-3y+3=0相离
所以 4<r<6
故答案为:(4,6)
点评:本题主要考查了圆与圆的位置关系和判定.考查了学生分析问题和数形结合思想的运用.要求学生有严密的逻辑思维能力.

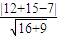 =4 到4x-3y+3=0距离是
=4 到4x-3y+3=0距离是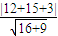 =6
=6 

 名校课堂系列答案
名校课堂系列答案