
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是矩形,平面
是矩形,平面![]() 平面
平面![]() 分别为棱
分别为棱![]() 的中点.求证:
的中点.求证:
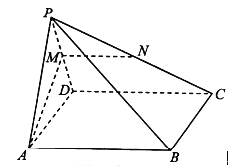
(1)![]() 平面
平面![]() ;
;
(2)![]() 平面
平面![]() .
.
【答案】(1)详见解析; (2)详见解析.
【解析】试题分析:(1)线面平行的证明则只需在面内找一线与之平行即可,因为M,N分别为棱PD,PC的中点,所以MN∥DC, 又因为底面ABCD是矩形,所以AB∥DC,
所以MN∥AB.(2)线面垂直则需要在面内找两根相交线与之垂直,因为AP=AD,M为PD的中点, 所以AM⊥PD.因为平面PAD⊥平面ABCD, 又平面PAD∩平面ABCD= AD,CD⊥AD,![]() 平面ABCD,所以CD⊥平面PAD. 又
平面ABCD,所以CD⊥平面PAD. 又![]() 平面PAD,所以CD⊥AM.
平面PAD,所以CD⊥AM.
试题解析:
(1)因为M,N分别为棱PD,PC的中点,所以MN∥DC, 又因为底面ABCD是矩形,所以AB∥DC,
所以MN∥AB. 又![]() 平面PAB,
平面PAB,![]() 平面PAB,所以MN∥平面PAB.
平面PAB,所以MN∥平面PAB.
(2)因为AP=AD,M为PD的中点, 所以AM⊥PD.因为平面PAD⊥平面ABCD, 又平面PAD∩平面ABCD= AD,CD⊥AD,![]() 平面ABCD,所以CD⊥平面PAD. 又
平面ABCD,所以CD⊥平面PAD. 又![]() 平面PAD,所以CD⊥AM. 因为CD,
平面PAD,所以CD⊥AM. 因为CD,![]() 平面PCD,
平面PCD,![]() ,所以AM⊥平面PCD.
,所以AM⊥平面PCD.


科目:高中数学 来源: 题型:
【题目】某赛季,甲、乙两名篮球运动员都参加了11场比赛,他们每场比赛得分的情况用如图所示的茎叶图表示,则甲、乙两名运动员的中位数分别为( ) 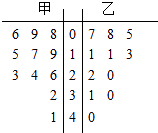
A.19、13
B.13、19
C.20、18
D.18、20
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙三人准备报考某大学,假设甲考上的概率为 ![]() ,甲,丙两都考不上的概率为
,甲,丙两都考不上的概率为 ![]() ,乙,丙两都考上的概率为
,乙,丙两都考上的概率为 ![]() ,且三人能否考上相互独立.
,且三人能否考上相互独立.
(1)求乙、丙两人各自考上的概率;
(2)设X表示甲、乙、丙三人中考上的人数与没考上的人数之差的绝对值,求X的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直角△ABC,AB=AC=3,P,Q分别为边AB,BC上的点,M,N是平面上两点,若 ![]() +
+ ![]() =0,(
=0,( ![]() +
+ ![]() )
) ![]() =0,
=0, ![]() =3
=3 ![]() ,且直线MN经过△ABC的外心,则
,且直线MN经过△ABC的外心,则 ![]() =( )
=( )
A.![]()
B.![]()
C.1
D.2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图已知四棱锥P﹣ABCD的底面ABCD是边长为2的正方形,PD⊥底面ABCD,E,F分别为棱BC,AD的中点. 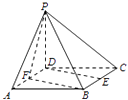
(1)若PD=1,求异面直线PB和DE所成角的余弦值.
(2)若二面角P﹣BF﹣C的余弦值为 ![]() ,求四棱锥P﹣ABCD的体积.
,求四棱锥P﹣ABCD的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com