
(5分)(2011•广东)设f(x),g(x),h(x)是R上的任意实值函数,如下定义两个函数(f°g)(x)和((f•g)(x)对任意x∈R,(f°g)(x)=f(g(x));(f•g)(x)=f(x)g(x),则下列等式恒成立的是( )
| A.((f°g)•h)(x)=((f•h)°(g•h))(x) |
| B.((f•g)°h)(x)=((f°h)•(g°h))(x) |
| C.((f°g)°h)(x)=((f°h)°(g°h))(x) |
| D.((f•g)•h)(x)=((f•h)•(g•h))(x) |
B
解析试题分析:根据定义两个函数(f°g)(x)和((f•g)(x)对任意x∈R,(f°g)(x)=f(g(x));(f•g)(x)=f(x)g(x),然后逐个验证即可找到答案.
解:A、∵(f°g)(x)=f(g(x)),(f•g)(x)=f(x)g(x),
∴((f°g)•h)(x)=(f°g)(x)h(x)=f(g(x))h(x);
而((f•h)°(g•h))(x)=(f•h)((g•h)(x))=f(g(x)h(x))h(g(x)h(x));
∴((f°g)•h)(x)≠((f•h)°(g•h))(x)
B、∵((f•g)°h)(x)=(f•g)(h(x))=f(h(x))g(h(x))
((f°h)•(g°h))(x)=(f°h)•(x)(g°h)(x)=f(h(x))g(h(x))
∴((f•g)°h)(x)=((f°h)•(g°h))(x)
C、((f°g)°h)(x)=((f°g)(h(x))=f(h(g(x))),
((f°h)°(g°h))(x)=f(h(g(h(x))))
∴((f°g)°h)(x)≠((f°h)°(g°h))(x);
D、((f•g)•h)(x)=f(x)g(x)h(x),
((f•h)•(g•h))(x)=f(x)h(x)g(x)h(x),
∴((f•g)•h)(x)≠((f•h)•(g•h))(x).
故选B.
点评:此题是个基础题.考查学生分析解决问题的能力,和知识方法的迁移能力.


 星级口算天天练系列答案
星级口算天天练系列答案科目:高中数学 来源: 题型:单选题
(2014·嘉兴模拟)已知a= ,b=0.3-2,c=lo
,b=0.3-2,c=lo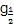 2,则a,b,c的大小关系是( )
2,则a,b,c的大小关系是( )
| A.a>b>c | B.a>c>b | C.c>b>a | D.b>a>c |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com