
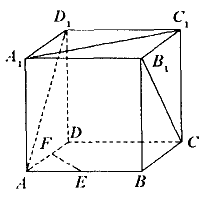
如图,正方体ABCD—∠A1B1C1D1中
(1)求A1C1与B1C所成角的大小;
(2)求A1C与AD1所成角的大小;
(3)若E、F分别为AB、AD的中点,求A1C1与EF所成角大小.
(4)求AD1与EF所成角大小.
|
思路 求异面直线所成的角关键是“找角”,在找角的过程中要多结合几何体的性质,尤其是正方体隐含着许多平行关系,另外中点又往往和中位线的性质紧密相连. 解答 (1)如图,连结AC,AB1,
由ABCD 知AA1C1C为平行四边形, 所以AC∥A1C1,从而B1C与AC所成的锐角或直角就是A1C1与B1C所成的角.AB1=AC=B1C可知∠B1CA= 即A1C1与B1C所成角为 (2)如图延长BC到M,使CM=BC,
连结D1M、AM,由BC∥A1D1且BC=A1D1, CM∥A1D1且CM=A1D1可知A1CMD1是平行四边形, 所以D1M∥A1C, 从而D1M与AD1所成的锐角或直角就是A1C与AD1所成角.设正方体的棱长为a,则AD1= AC1= 由余弦定理可知cos∠AD1M= 所以∠AD1M= 另解∵CD⊥平面A1D ∴直线A1C在平面A1D内的射影为直线A1D 又∵A1D⊥AD1, ∴由三垂线定理可知A1C⊥AD1 ∴A1C与AD1所成角为 (3)如图连结AC、BD,由AA1∥CC1,且AA1=CC1可知A1ACC1是平行四边形,
∴AC∥A1C1 ∴AC是与EF所成的锐角或直角就是A1C1与EF所成的角 ∵EF是△ABD的中位线 ∴EF∥BD 又∵AC⊥BD, ∴EF⊥AC,即所求角为 (4)如图连结BD、B1D1,由DD1∥BB1且DD1=BB1可知B1BDD1是平行四边形,∴BD∥B1D1
∴AD1与B1D1所成的锐角或直角即为AD1与EF所成角 连结AB1,由AB1=AD1=B1D1, 知△AB1D1是正三角形 ∴∠AD1B1= 评析 求两条异面直线所成的角需将两条异面直线所成的角转化为两条相交直线所成的锐角或直角,这一过程一般是通过平移或补形实现的,并且尽量以平移为主.在平移的过程中,有时不可能一次实现,这时需多结合几何体(本题为正方体)的性质.另外,有些问题表面看来虽然是成角问题,但实际上是垂直问题,例如第(2)问,利用三垂线定理(参看另解)非常简捷. |


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
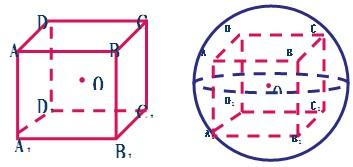
 如图,正方体ABCD-A1B1C1D1棱长为8,E、F分别为AD1,CD1中点,G、H分别为棱DA,DC上动点,且EH⊥FG.
如图,正方体ABCD-A1B1C1D1棱长为8,E、F分别为AD1,CD1中点,G、H分别为棱DA,DC上动点,且EH⊥FG.查看答案和解析>>
科目:高中数学 来源: 题型:
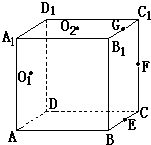 如图,正方体ABCD-A1B1C1D1中,若E、F、G分别为棱BC、C1C、B1C1的中点,O1、O2分别为四边形ADD1A1、A1B1C1D1的中心,则下列各组中的四个点不在同一个平面上的是( )
如图,正方体ABCD-A1B1C1D1中,若E、F、G分别为棱BC、C1C、B1C1的中点,O1、O2分别为四边形ADD1A1、A1B1C1D1的中心,则下列各组中的四个点不在同一个平面上的是( )查看答案和解析>>
科目:高中数学 来源: 题型:
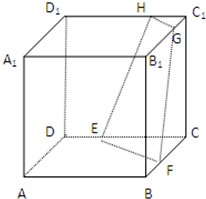 如图,正方体ABCD-A1B1C1D1中,E、F、G、H分别是所在棱的三等分点,且BF=DE=C1G=C1H=
如图,正方体ABCD-A1B1C1D1中,E、F、G、H分别是所在棱的三等分点,且BF=DE=C1G=C1H=| 1 | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com