
【题目】某单位员工![]() 人参加“学雷锋”志愿活动,按年龄分组:第
人参加“学雷锋”志愿活动,按年龄分组:第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.

(1)下表是年龄的频率分布表,求正整数![]() 的值;
的值;
区间 |
|
|
|
|
|
人数 |
|
|
|
|
|
(2)现在要从年龄较小的第![]() 组中用分层抽样的方法抽取
组中用分层抽样的方法抽取![]() 人,年龄在第
人,年龄在第![]() 组抽取的员工的人数分别是多少?
组抽取的员工的人数分别是多少?
(3)在(2)的前提下,从这![]() 人中随机抽取
人中随机抽取![]() 人参加社区宣传交流活动,求至少有
人参加社区宣传交流活动,求至少有![]() 人年龄在第
人年龄在第![]() 组的概率.
组的概率.
【答案】(1)![]() ,
,![]() (2)
(2)![]() 人,
人,![]() 人,
人,![]() 人. (3)
人. (3)![]()
【解析】
(I)由题意可知![]() ,
,![]() .
.
(II)根据各层在总体当中的占比与在样本中的占比相等,求出年龄在第1,2,3组的人数. 因为第1,2,3组共有50+50+200=300人,
利用分层抽样在300名学生中抽取![]() 名学生,每组抽取的人数分别为:
名学生,每组抽取的人数分别为:
第1组的人数为![]() , 第2组的人数为
, 第2组的人数为![]() ,
,
第3组的人数为![]() , 所以第1,2,3组分别抽取1人,1人,4人.……6分
, 所以第1,2,3组分别抽取1人,1人,4人.……6分
(III) 设第1组的1位同学为![]() ,第2组的1位同学为
,第2组的1位同学为![]() ,第3组的4位同学为
,第3组的4位同学为![]() ,则从六位同学中抽两位同学有15种可能.其中2人年龄都不在第3组的有1种可能.
,则从六位同学中抽两位同学有15种可能.其中2人年龄都不在第3组的有1种可能.
所以至少有1人年龄在第3组的概率为![]() .设第1组的1位同学为
.设第1组的1位同学为![]() ,第2组的1位同学为
,第2组的1位同学为![]() ,第3组的4位同学为
,第3组的4位同学为![]() ,则从六位同学中抽两位同学有:
,则从六位同学中抽两位同学有:
![]()
![]()
![]()
![]()
![]()
![]() 共
共![]() 种可能. ………………10分
种可能. ………………10分
其中2人年龄都不在第3组的有:![]() 共1种可能, ………………11分
共1种可能, ………………11分
所以至少有1人年龄在第3组的概率为![]() . ………………12分
. ………………12分


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2cos( ![]() ﹣x)sinx+(sinx+cosx)2 .
﹣x)sinx+(sinx+cosx)2 .
(1)求函数f(x)的单调递增区间;
(2)把y=f(x)的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图象向左平移 ![]() 个单位,得到函数y=g(x)的图象,求
个单位,得到函数y=g(x)的图象,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】调查某医院某段时间内婴儿出生的时间与性别的关系,得到下面的数据:出生时间在晚上的男婴为24人,女婴为8人;出生时间在白天的男婴为31人,女婴为26人.
(1)将2×2列联表补充完整.
性别 | 出生时间 | 总计 | |
晚上 | 白天 | ||
男婴 | |||
女婴 | |||
总计 | |||
(2)能否在犯错误的概率不超过0.1的前提下认为婴儿性别与出生时间有关系?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知球O是正三棱锥(底面为正三角形,顶点在底面的射影为底面中心)A﹣BCD的外接球,BC=3,AB=2 ![]() ,点E在线段BD上,且BD=3BE,过点E作球O的截面,则所得截面圆面积的取值范围是 .
,点E在线段BD上,且BD=3BE,过点E作球O的截面,则所得截面圆面积的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)的长轴长为6,且椭圆C与圆M:(x﹣2)2+y2=
=1(a>b>0)的长轴长为6,且椭圆C与圆M:(x﹣2)2+y2= ![]() 的公共弦长为
的公共弦长为 ![]() .
.
(1)求椭圆C的方程,
(2)过点P(0,2)作斜率为k(k≠0)的直线l与椭圆C交于两点A,B,试判断在x轴上是否存在点D,使得△ADB为以AB为底边的等腰三角形,若存在,求出点D的横坐标的取值范围,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年备受瞩目的二十国集团领导人第十一次峰会于9月4~5日在杭州举办,杭州G20筹委会已经招募培训翻译联络员1000人、驾驶员2000人,为测试培训效果,采取分层抽样的方法从翻译联络员、驾驶员中共随机抽取60人,对其做G20峰会主题及相关服务职责进行测试,将其所得分数(分数都在60~100之间)制成频率分布直方图如下图所示,若得分在90分及其以上(含90分)者,则称其为“G20通”. 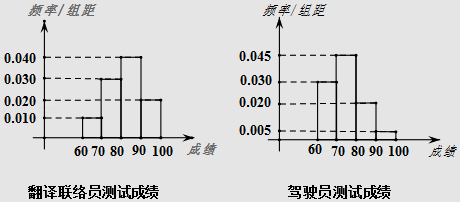
(Ⅰ)能否有90%的把握认为“G20通”与所从事工作(翻译联络员或驾驶员)有关?
(Ⅱ)从参加测试的成绩在80分以上(含80分)的驾驶员中随机抽取4人,4人中“G20通”的人数为随机变量X,求X的分布列与数学期望.
P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 6.635 | 10.828 |
附参考公式与数据: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sin2( ![]() +x)﹣
+x)﹣ ![]() cos2x﹣1,x∈R,若函数k(x)=f(x+a)的图象关于点(﹣
cos2x﹣1,x∈R,若函数k(x)=f(x+a)的图象关于点(﹣ ![]() ,0)对称,且α∈(0,π),则α=( )
,0)对称,且α∈(0,π),则α=( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com