考点:利用导数求闭区间上函数的最值,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(1)求函数的导数,根据导数的几何意义建立条件关系即可求实数a的值及f(x)的极值;
(2)根据不等式单调函数的单调性关系,将不等式进行转化,利用导数求函数的最值即可得到结论.
解答:
解:(1)函数的f(x)的导数f′(x)=
=
,
∵f(x)在点(1,f(1))处的切线与x轴平行,
∴f′(0)=
=0,
∴a=1,
∴f(x)=
,x>0,f′(x)=-
,
当0<x<1时,f′(x)>0,当x>1时,f′(x)<0
∴f(x)在(0,1)上单调递增,在(1,+∞)单调递减,
故f(x)在x=1处取得极大值1,无极小值
(2)由(1)的结论知,f(x)在[e
2,+∞)上单调递减,不妨设x
1≥x
2≥e
2,
则|f(x
1)-f(x
2)|≥k|
-
|,?f(x
2)-f(x
1)≥k(
-
),
?f(x
2)-k•
≥f(x
1)-k•
,
?函数F(x)=f(x)-
=
-在[e
2,+∞)上单调递减,
则F′(x)=
≤0在[e
2,+∞)上恒成立,
∴k≤lnx在[e
2,+∞)上恒成立,
在[e
2,+∞)上,(lnx)
min=lne
2=2,
故k≤2.
点评:本题主要考查导数的综合应用,根据导数的几何意义求出a,以及函数极值,最值和导数之间的关系是解决本题的关键.



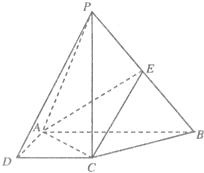 如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2,BC=
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2,BC=