
【题目】已知函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)当![]() 时,证明:对任意的
时,证明:对任意的![]() ,有
,有![]() .
.
【答案】(1)答案见解析;(2)证明见解析.
【解析】试题分析:
(1)由题意结合导函数的解析式分类讨论有:
当![]() 时,
时, ![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
当![]() 时,
时, ![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
当![]() 时,
时, ![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时, ![]() 在
在![]() 和
和![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
(2)原问题等价于![]() 在
在![]() 上恒成立,构造函数
上恒成立,构造函数![]() ,据此可得
,据此可得![]() ,则
,则![]() 恒成立.
恒成立.
试题解析:
(1)由题意得![]() ,
,
当![]() 时,由
时,由![]() 得
得![]() 且
且![]() ,
,
则
①当![]() 时,
时, ![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
②当![]() 时,
时, ![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
③当![]() 时,
时, ![]() 在
在![]() 上单调递增;
上单调递增;
④当![]() 时,
时, ![]() 在
在![]() 和
和![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
(2)当![]() 时,要证
时,要证![]() 在
在![]() 上恒成立,
上恒成立,
只需证![]() 在
在![]() 上恒成立,
上恒成立,
令![]() ,
,
因为![]() ,
,
易得![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,故
上单调递减,故![]() ,
,
由得![]() ,得
,得![]() ,
,
当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() ,
,
所以![]() ,
,
又![]() ,所以
,所以![]() ,即
,即![]() ,
,
所以![]() 在
在![]() 上恒成立,
上恒成立,
故当![]() 时,对任意的
时,对任意的![]() ,
, ![]() 恒成立.
恒成立.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中数学 来源: 题型:
【题目】如图,在三棱锥D﹣ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC=a,E为BC点,F棱AC上,且AF=3FC. 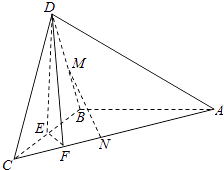
(1)求三棱锥D﹣ABC的体积;
(2)求证:AC⊥平面DEF;
(3)若M为DB中点,N在棱AC上,且CN= ![]() CA,求证:MN∥平面DEF.
CA,求证:MN∥平面DEF.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在直角梯形ABCD中,AB∥CD,∠BCD=90°,BC=CD=2,AF=BF,EC∥FD,FD⊥底面ABCD,M是AB的中点. 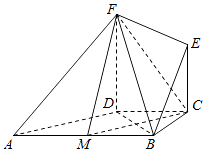
(1)求证:平面CFM⊥平面BDF;
(2)点N在CE上,EC=2,FD=3,当CN为何值时,MN∥平面BEF.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,四棱锥P﹣ABCD的底面ABCD是边长为1的菱形,∠BCD=60°,E是CD的中点,PA⊥底面ABCD,PA=2. (Ⅰ)证明:平面PBE⊥平面PAB;
(Ⅱ)求二面角B﹣PE﹣D的余弦值.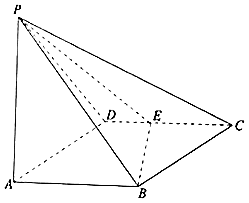
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,△ABC为正三角形,AB⊥AD,AC⊥CD,PA⊥平面ABCD,PC与平面ABCD所成角为45° 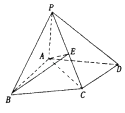
(1)若E为PC的中点,求证:PD⊥平面ABE;
(2)若CD= ![]() ,求点B到平面PCD的距离.
,求点B到平面PCD的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若圆C1:(x﹣1)2+(y+3)2=1与圆C2:(x﹣a)2+(y﹣b)2=1外离,过直线l:x﹣y﹣1=0上任意一点P分别做圆C1 , C2的切线,切点分别为M,N,且均保持|PM|=|PN|,则a+b=( )
A.﹣2
B.﹣1
C.1
D.2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区有小学21所,中学14所,大学7所,现采用分层抽样的方法从这些学校中抽取6所学校对学生进行视力调查.
(1)求应从小学、中学、大学中分别抽取的学校数目;
(2)若从抽取的6所学校中随机抽取2所学校做进一步数据分析. (ⅰ)列出所有可能的抽取结果;
(ⅱ)求抽取的2所学校均为小学的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD﹣A1B1C1D1中,点O为线段BD的中点,设点P在线段CC1上,直线OP与平面A1BD所成的角为α,则sinα的取值范围是( ) 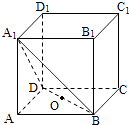
A.[ ![]() ,1]
,1]
B.[ ![]() ,1]
,1]
C.[ ![]() ,
, ![]() ]
]
D.[ ![]() ,1]
,1]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB是圆O的直径,PA垂直圆所在的平面,C是圆上的点. 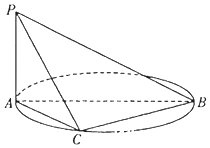
(I)求证:平面PAC⊥平面PBC;
(II)若AC=1,PA=1,求圆心O到平面PBC的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com