
分析 (1)求出椭圆的短轴长,然后求解椭圆方程.
(2)利用双曲线的离心率求出实半轴的长,求出虚半轴的长,即可求解双曲线方程.
解答 解:(1):椭圆焦距为8,长半轴长为10,焦点在x轴上,可得c=4,a=5,则b=3,
椭圆的标准方程为:$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{9}=1$.
(2)双曲线C的右焦点为F(3,0),可得c=3,e=$\frac{3}{2}$,故a=2,b=$\sqrt{c2-a2}$=$\sqrt{5}$,
故双曲线方程为$\frac{x2}{4}$-$\frac{y2}{5}$=1.
点评 本题考查椭圆的简单性质,双曲线的简单性质,方程的求法,考查计算能力.


科目:高中数学 来源: 题型:解答题
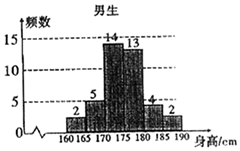 为了解学生身高情况,某校以10%的比例对全校700名学生按性别进行分层抽样检查,测得身高情况的统计图如下:
为了解学生身高情况,某校以10%的比例对全校700名学生按性别进行分层抽样检查,测得身高情况的统计图如下:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
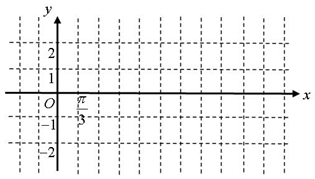
| x | -$\frac{π}{3}$ | $\frac{2π}{3}$ | $\frac{5π}{3}$ | $\frac{8π}{3}$ | $\frac{11π}{3}$ |
| $\frac{1}{2}x+\frac{π}{6}$ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| y | 0 | 2 | 0 | -2 | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 某几何体的正视图和侧视图如图①,它的俯视图的直观图为矩形O1A1B1C1如图②,其中O1A1=6,O1C1=2,则该几何体的体积为( )
某几何体的正视图和侧视图如图①,它的俯视图的直观图为矩形O1A1B1C1如图②,其中O1A1=6,O1C1=2,则该几何体的体积为( )| A. | 16$\sqrt{2}$ | B. | 32$\sqrt{2}$ | C. | 32 | D. | 64 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com