
【题目】如图,在四棱锥P﹣ABCD中,直线PA⊥平面ABCD,AD∥BC,AB⊥AD,BC=2AB=2AD=4BE=4.
(I)求证:直线DE⊥平面PAC.
(Ⅱ)若直线PE与平面PAC所成的角的正弦值为 ![]() ,求二面角A﹣PC﹣D的平面角的余弦值.
,求二面角A﹣PC﹣D的平面角的余弦值.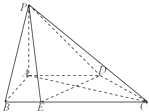
【答案】解:(Ⅰ)∵PA⊥平面ABCD,∴AB⊥PA.又∵AB⊥AD,故可建立建立如图所示坐标系.由已知D(0,2,0),E(2,1,0),C(2,4,0),P(0,0,λ),(λ>0), ![]() =(2,﹣1,0),
=(2,﹣1,0),![]() =(2,4,0),
=(2,4,0), ![]() =(0,0,λ),
=(0,0,λ),![]() =4﹣4+0=0,
=4﹣4+0=0, ![]() =0.
=0.
∴DE⊥AC,DE⊥AP,
∴ED⊥平面PAC.
(Ⅱ)由(Ⅰ),平面PAC的一个法向量是 ![]() ,
, ![]() =(2,1,λ).
=(2,1,λ).
设直线PE与平面PAC所成的角为θ,
∴sinθ=|cos ![]() |=
|= ![]() =
= ![]() ,
,
解得λ=±2,∵λ>0,∴λ=2,即P(0,0,2).
设平面PCD的一个法向量为 ![]() =(x,y,z),
=(x,y,z), ![]() =(2,2,0),
=(2,2,0), ![]() =(0,﹣2,﹣2),
=(0,﹣2,﹣2),
∴  ,∴
,∴ ![]() ,取
,取 ![]() =(1,﹣1,﹣1).
=(1,﹣1,﹣1).
∴cos ![]() =
= ![]() =
= ![]() ,
,
显然二面角A﹣PC﹣D的平面角是锐角,∴二面角A﹣PC﹣D的平面角的余弦值为 ![]() .
.
【解析】(Ⅰ)由PA⊥平面ABCD,可得AB⊥PA.又AB⊥AD,可建立建立如图所示坐标系.利用向量垂直与数量积的关系、线面垂直的判定定理即可得出.(Ⅱ)由(Ⅰ),平面PAC的一个法向量是 ![]() ,
, ![]() =(2,1,λ).设直线PE与平面PAC所成的角为θ,可得sinθ=|cos
=(2,1,λ).设直线PE与平面PAC所成的角为θ,可得sinθ=|cos ![]() |=
|=  ,解得λ.设平面PCD的一个法向量为
,解得λ.设平面PCD的一个法向量为 ![]() =(x,y,z),
=(x,y,z),  ,可得cos
,可得cos ![]() =
=  .
.


 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:高中数学 来源: 题型:
【题目】已知四棱锥P﹣ABCD的底面ABCD是平行四边形,△PAB与△ABC是等腰三角形,PA⊥平面ABCD,PA=2,AD=2 ![]() ,AC⊥BA,点E是线段AB上靠近点B的一个三等分点,点F、G分别在线段PD,PC上.
,AC⊥BA,点E是线段AB上靠近点B的一个三等分点,点F、G分别在线段PD,PC上. 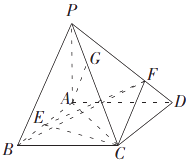
(Ⅰ)证明:CD⊥AG;
(Ⅱ)若三棱锥E﹣BCF的体积为 ![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系xoy中,椭圆C1: ![]() +
+ ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,过椭圆右焦点F作两条相互垂直的弦,当其中一条弦所在直线斜率为0时,两弦长之和为6.
,过椭圆右焦点F作两条相互垂直的弦,当其中一条弦所在直线斜率为0时,两弦长之和为6.
(1)求椭圆的方程;
(2)A,B是抛物线C2:x2=4y上两点,且A,B处的切线相互垂直,直线AB与椭圆C1相交于C,D两点,求弦|CD|的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ln(1+|x|)﹣ ![]() ,则使得f(x)>f(2x﹣1)成立的取值范围是( )
,则使得f(x)>f(2x﹣1)成立的取值范围是( )
A.(﹣∞, ![]() )∪(1,+∞)
)∪(1,+∞)
B.( ![]() ,1)
,1)
C.( ![]() )
)
D.(﹣∞,﹣ ![]() ,)
,) ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若存在实常数k和b,使得函数F(x)和G(x)对其公共定义域上的任意实数x都满足:F(x)≥kx+b和G(x)≤kx+b恒成立,则称此直线y=kx+b为F(x)和G(x)的“隔离直线”,已知函数f(x)=x2(x∈R),g(x)= ![]() (x<0),h(x)=2elnx,有下列命题:
(x<0),h(x)=2elnx,有下列命题:
①F(x)=f(x)﹣g(x)在 ![]() 内单调递增;
内单调递增;
②f(x)和g(x)之间存在“隔离直线”,且b的最小值为﹣4;
③f(x)和g(x)之间存在“隔离直线”,且k的取值范围是(﹣4,0];
④f(x)和h(x)之间存在唯一的“隔离直线”y=2 ![]() x﹣e.
x﹣e.
其中真命题的个数为(请填所有正确命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某网店经营的一种商品进行进价是每件10元,根据一周的销售数据得出周销售量![]() (件)与单价
(件)与单价![]() (元)之间的关系如下图所示,该网店与这种商品有关的周开支均为25元.
(元)之间的关系如下图所示,该网店与这种商品有关的周开支均为25元.
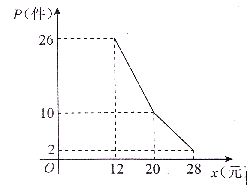
(1)根据周销售量图写出![]() (件)与单价
(件)与单价![]() (元)之间的函数关系式;
(元)之间的函数关系式;
(2)写出利润![]() (元)与单价
(元)与单价![]() (元)之间的函数关系式;当该商品的销售价格为多少元时,周利润最大?并求出最大周利润.
(元)之间的函数关系式;当该商品的销售价格为多少元时,周利润最大?并求出最大周利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两名射击运动员分别对一个目标射击1次,甲射中的概率为![]() ,乙射中的概率为
,乙射中的概率为![]() ,求:
,求:
(1)2人中恰有1人射中目标的概率;
(2)2人至少有1人射中目标的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,AB= ![]() ,BC=1,P为△ABC内一点,∠BPC=90°
,BC=1,P为△ABC内一点,∠BPC=90° 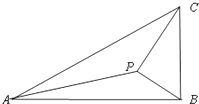
(1)若PB= ![]() ,求PA;
,求PA;
(2)若∠APB=150°,求tan∠PBA.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com