
【题目】在平面直角坐标系xOy中,已知直线l的普通方程为x﹣y﹣2=0,曲线C的参数方程为 ![]() (θ为参数),设直线l与曲线C交于A,B两点.若点P在曲线C上运动,当△PAB的面积最大时,求点P的坐标及△PAB的最大面积.
(θ为参数),设直线l与曲线C交于A,B两点.若点P在曲线C上运动,当△PAB的面积最大时,求点P的坐标及△PAB的最大面积.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,正四面体ABCD的顶点C在平面α内,且直线BC与平面α所成角为15°,顶点B在平面α上的射影为点O,当顶点A与点O的距离最大时,直线CD与平面α所成角的正弦值为 . 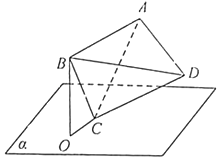
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一块以点O为圆心,半径为2百米的圆形草坪,草坪内距离O点 ![]() 百米的D点有一用于灌溉的水笼头,现准备过点D修一条笔直小路交草坪圆周于A,B两点,为了方便居民散步,同时修建小路OA,OB,其中小路的宽度忽略不计.
百米的D点有一用于灌溉的水笼头,现准备过点D修一条笔直小路交草坪圆周于A,B两点,为了方便居民散步,同时修建小路OA,OB,其中小路的宽度忽略不计.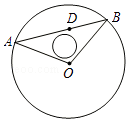
(1)若要使修建的小路的费用最省,试求小路的最短长度;
(2)若要在△ABO区域内(含边界)规划出一块圆形的场地用于老年人跳广场舞,试求这块圆形广场的最大面积.(结果保留根号和π)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】公比为q(q≠1)的等比数列a1 , a2 , a3 , a4 , 若删去其中的某一项后,剩余的三项(不改变原有顺序)成等差数列,则所有满足条件的q的取值的代数和为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数 ![]() (ω>0)的图象与x轴正半轴交点的横坐标构成一个公差为
(ω>0)的图象与x轴正半轴交点的横坐标构成一个公差为 ![]() 的等差数列,若要得到函数g(x)=Asinωx的图象,只要将f(x)的图象( )个单位.
的等差数列,若要得到函数g(x)=Asinωx的图象,只要将f(x)的图象( )个单位.
A.向左平移 ![]()
B.向右平移 ![]()
C.向左平移 ![]()
D.向右平移 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数y= ![]() 与y=ln(1﹣x)的定义域分别为M、N,则M∪N=( )
与y=ln(1﹣x)的定义域分别为M、N,则M∪N=( )
A.(1,2]
B.[1,2]
C.(﹣∞,1]∪(2,+∞)
D.(﹣∞,1)∪[2,+∞)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com