
【题目】如图, ![]() 是圆柱的母线,
是圆柱的母线, ![]() 是
是 ![]() 的直径,
的直径, ![]() 是底面圆周上异于
是底面圆周上异于 ![]() 的任意一点,
的任意一点, ![]() ,
, ![]() .
.
(1)求证: ![]()
(2)当三棱锥 ![]() 的体积最大时,求
的体积最大时,求 ![]() 与平面
与平面 ![]() 所成角的大小;
所成角的大小;
(3)![]() 上是否存在一点
上是否存在一点 ![]() ,使二面角
,使二面角 ![]() 的平面角为45°?若存在,求出此时
的平面角为45°?若存在,求出此时 ![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
【答案】
(1)解:∵ ![]() 平面
平面 ![]() ,
, ![]() 平面
平面 ![]()
∴ ![]() ,又
,又 ![]() ,
, ![]()
∴ ![]() 平面
平面 ![]()
又∵ ![]() 平面
平面 ![]() ,
,
∴平面 ![]() 平面
平面 ![]() ,
,
而平面 ![]() 平面
平面 ![]() ,
, ![]()
∴ ![]() 平面
平面 ![]() ,而
,而 ![]() 平面
平面 ![]() ,
,
∴ ![]()
(2)解:设 ![]() ,在
,在 ![]() 中,
中, ![]()
∵ ![]() 平面
平面 ![]() ,
,
∴ ![]() 是三棱锥
是三棱锥 ![]() 的高
的高
因此三棱锥 ![]() 的体积为
的体积为![]()
![]()
![]()
∵ ![]() ,
, ![]() ,
,
∴当 ![]() ,即
,即 ![]() 时,三棱锥
时,三棱锥 ![]() 体积的最大值为
体积的最大值为 ![]()
此时 ![]() 为等腰直角三角形,
为等腰直角三角形,
∴ ![]() 与平面
与平面 ![]() 所成角度为45°
所成角度为45°
(3)解:存在这样的点 ![]() 且
且 ![]() ,理由如下:
,理由如下:
记 ![]() 的中点为
的中点为 ![]() ,连接
,连接 ![]() ,
,
∵ ![]() 为等腰直角三角形
为等腰直角三角形
∴ ![]() ,由(1)知
,由(1)知 ![]() ,
, ![]()
∴ ![]() 平面
平面 ![]() ,
,
又 ![]() 平面
平面 ![]() ,∴
,∴ ![]()
∴ ![]() 是二面角
是二面角 ![]() 的平面角,即
的平面角,即 ![]()
![]() 为等腰直角三角形,
为等腰直角三角形, ![]() ,
,
∴ ![]()
在 ![]() 中,
中, ![]()
在 ![]() 和
和 ![]() 中,可解得
中,可解得 ![]() ,
, ![]()
【解析】(1)根据圆的直径所对圆周角为直角,以及SA与平面ABC垂直的性质,得到直线BC与平面SAC垂直,证明平面SBC与平面SAC垂直,再利用线面垂直的性质证明结论。
(2)设 AC=x ,用x表示出三棱锥S-ABC的体积,利用二次函数的最值问题,求出结果。
(3)取SB的中点E,分别连接AE,DE,根据AD与平面SBC垂直,AD与SB垂直,证明SB与平面ADE垂直,证明 是二面角 A-SB-C 的平面角,求出结果。


 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:
【题目】椭圆 ![]() (a>b>0)与x轴,y轴的正半辆分别交于A,B两点,原点O到直线AB的距离为
(a>b>0)与x轴,y轴的正半辆分别交于A,B两点,原点O到直线AB的距离为 ![]() ,该椭圆的离心率为
,该椭圆的离心率为 ![]() . (Ⅰ)求椭圆的方程;
. (Ⅰ)求椭圆的方程;
(Ⅱ)过点 ![]() 的直线l与椭圆交于两个不同的点M,N,求线段MN的垂直平分线在y轴上截距的取值范围.
的直线l与椭圆交于两个不同的点M,N,求线段MN的垂直平分线在y轴上截距的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2px(p>0)的焦点为F,直线y=4与y轴的交点为P,与C的交点为Q,且|QF|= ![]() |PQ|. (Ⅰ)求C的方程;
|PQ|. (Ⅰ)求C的方程;
(Ⅱ)过F的直线l与C相交于A、B两点,若AB的垂直平分线l′与C相交于M、N两点,且A、M、B、N四点在同一圆上,求l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为 ![]()

(1)求频率分布图中 ![]() 的值,并估计该企业的职工对该部门评分不低于80的概率;
的值,并估计该企业的职工对该部门评分不低于80的概率;
(2)从评分在 ![]() 的受访职工中,随机抽取2人,求此2人评分都在
的受访职工中,随机抽取2人,求此2人评分都在 ![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一台机器由于使用时间较长,生产的零件有一些缺损,按不同转速生产出来的零件有缺损的统计数据如下表所示.
转速x(转/秒) | 16 | 14 | 12 | 8 |
每小时生产有缺损零件数y(个) | 11 | 9 | 8 | 5 |
(1)作出散点图;
(2)如果y与x线性相关,求出回归直线方程;
(3)若实际生产中,允许每小时的产品中有缺损的零件最多为10个,那么机器的运转速度应控制在什么范围内?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校做了一次关于“感恩父母”的问卷调查,从8~10岁,11~12岁,13~14岁,15~16岁四个年龄段回收的问卷依次为:120份,180份,240份,x份.因调查需要,从回收的问卷中按年龄段分层抽取容量为300的样本,其中在11~12岁学生问卷中抽取60份,则在15~16岁学生中抽取的问卷份数为( )
A.60
B.80
C.120
D.180
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的右焦点为F(1,0),且点
的右焦点为F(1,0),且点 ![]() 在椭圆C上,O为坐标原点. (Ⅰ)求椭圆C的标准方程;
在椭圆C上,O为坐标原点. (Ⅰ)求椭圆C的标准方程;
(Ⅱ)设过定点T(0,2)的直线l与椭圆C交于不同的两点A、B,且∠AOB为锐角,求直线l的斜率k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知PA⊥平面ABCD,且四边形ABCD为矩形,M、N分别是AB、PC的中点.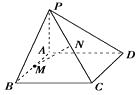
(1)求证:MN⊥CD;
(2)若∠PDA=45°,求证:MN⊥平面PCD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com