
【题目】某校李老师本学期任高一A班、B班两个班数学课教学,两个班都是50个学生,下图反映的是两个班在本学期5次数学检测中的班级平均分对比,根据图表信息,下列不正确的结论是( )

A. A班的数学成绩平均水平好于B班
B. B班的数学成绩没有A班稳定
C. 下次B班的数学平均分高于A班
D. 在第一次考试中,A、B两个班总平均分为78分
 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:
【题目】如图,海岸公路MN的北方有一个小岛A(大小忽略不计)盛产海产品,在公路MN的B处有一个海产品集散中心,点C在B的正西方向10![]() 处,
处,![]() ,
,![]() ,计划开辟一条运输线将小岛的海产品运送到集散中心.现有两种方案:①沿线段AB开辟海上航线:②在海岸公路MN上选一点P建一个码头,先从海上运到码头,再公路MN运送到集散中心.已知海上运输、岸上运输费用分别为400元/
,计划开辟一条运输线将小岛的海产品运送到集散中心.现有两种方案:①沿线段AB开辟海上航线:②在海岸公路MN上选一点P建一个码头,先从海上运到码头,再公路MN运送到集散中心.已知海上运输、岸上运输费用分别为400元/![]() 、200元/
、200元/![]() .
.
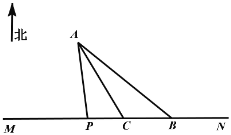
(1)求方案①的运输费用;
(2)请确定P点的位置,使得按方案②运送时运输费用最低?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C1的极坐标方程为ρsinθ=2.
(1)M为曲线C1上的动点,点P在线段OM上,且满足![]() ,求点P的轨迹C2的直角坐标方程;
,求点P的轨迹C2的直角坐标方程;
(2)曲线C2上两点![]() 与点B(ρ2,α),求△OAB面积的最大值.
与点B(ρ2,α),求△OAB面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《高中数学课程标准》(2017版)规定了数学直观想象学科的六大核心素养,为了比较甲、乙两名高二学生的数学核心素养水平,现以六大素养为指标对二人进行了测验,根据测验结果绘制了雷达图(如图,每项指标值满分为5分,分值高者为优),则下面叙述正确的是(注:雷达图![]() ,又可称为戴布拉图、蜘蛛网图
,又可称为戴布拉图、蜘蛛网图![]() ,可用于对研究对象的多维分析)( )
,可用于对研究对象的多维分析)( )
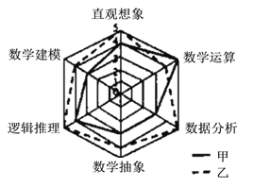
A.甲的直观想象素养高于乙
B.甲的数学建模素养优于数据分析素养
C.乙的数学建模素养与数学运算素养一样
D.乙的六大素养整体水平低于甲
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】台球运动已有五、六百年的历史,参与者用球杆在台上击球.若和光线一样,台球在球台上碰到障碍物后也遵从反射定律如图,有一张长方形球台ABCD,![]() ,现从角落A沿角
,现从角落A沿角![]() 的方向把球打出去,球经2次碰撞球台内沿后进入角落C的球袋中,则
的方向把球打出去,球经2次碰撞球台内沿后进入角落C的球袋中,则![]() 的值为( )
的值为( )
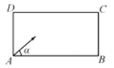
A.![]() B.
B.![]() C.1D.
C.1D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面上一动点A的坐标为![]() .
.
(1)求点A的轨迹E的方程;
(2)点B在轨迹E上,且纵坐标为![]() .
.
(i)证明直线AB过定点,并求出定点坐标;
(ii)分别以A,B为圆心作与直线![]() 相切的圆,两圆公共弦的中点为H,在平面内是否存在定点P,使得
相切的圆,两圆公共弦的中点为H,在平面内是否存在定点P,使得![]() 为定值?若存在,求出点P坐标;若不存在,请说明理由.
为定值?若存在,求出点P坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
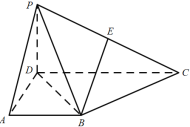
【题目】
在四棱锥![]() 中,侧面
中,侧面![]() 底面
底面![]() ,
,![]() ,
,![]() 为
为![]() 中点,底面
中点,底面![]() 是直角梯形,
是直角梯形,![]() ,
,![]() =90°,
=90°,![]() ,
,![]() .
.
(I)求证:![]()
![]() 平面
平面![]() ;
;
(II)求证:![]() 平面
平面![]() ;
;
(III)设![]() 为侧棱
为侧棱![]() 上一点,
上一点,![]() ,试确定
,试确定![]() 的值,使得二面角
的值,使得二面角![]() 为45°.
为45°.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种水果按照果径大小可分为四类:标准果,优质果,精品果,礼品果.某采购商从采购的一批水果中随机抽取100个,利用水果的等级分类标准得到的数据如下:
等级 | 标准果 | 优质果 | 精品果 | 礼品果 |
个数 | 10 | 30 | 40 | 20 |
(1)用样本估计总体,果园老板提出两种购销方案给采购商参考:
方案1:不分类卖出,单价为20元/![]() .
.
方案2:分类卖出,分类后的水果售价如下表:
等级 | 标准果 | 优质果 | 精品果 | 礼品果 |
售价(元/ | 16 | 18 | 22 | 24 |
从采购商的角度考虑,应该采用哪种方案较好?并说明理由.
(2)从这100个水果中用分层抽样的方法抽取10个,再从抽取的10个水果中随机抽取3个,![]() 表示抽取到精品果的数量,求
表示抽取到精品果的数量,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com