
����Ŀ��ij��УΪ����Ӧ���ҵ����ҵ���ᣬÿ�����Ӧ���ҵ�����ۺ����ʺ�ѧҵ�ɼ���ѧ�������ۺ���������֪ij��Ȳ��������ı�ҵ������2000�����������ɼ�![]() ���Ƶķ�����̬�ֲ�
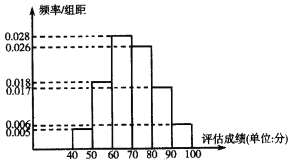
���Ƶķ�����̬�ֲ�![]() ���������ȡ��100����ҵ���������ɼ���Ϊ�����������������ݽ����˷��飬����������Ƶ�ʷֲ�ֱ��ͼ��
���������ȡ��100����ҵ���������ɼ���Ϊ�����������������ݽ����˷��飬����������Ƶ�ʷֲ�ֱ��ͼ��
��1��������ƽ����![]() ����������
����������![]() ��ͬһ���е������ø���������е�ֵ����������
��ͬһ���е������ø���������е�ֵ����������
��2����ѧУ�涨�����ɼ�����82.7�ֵı�ҵ���ɲμ�![]() ���ҹ�˾�����ԣ�
���ҹ�˾�����ԣ�
������ƽ����![]() ��Ϊ�Ĺ���ֵ
��Ϊ�Ĺ���ֵ![]() ������������
������������![]() ��Ϊ
��Ϊ![]() �Ĺ���ֵ
�Ĺ���ֵ![]() �������ù���ֵ�ж���2000����ҵ���У��ܹ��μ����ҹ�˾���Ե�������
�������ù���ֵ�ж���2000����ҵ���У��ܹ��μ����ҹ�˾���Ե�������
����![]() ���������
���������![]() ����
����![]() ��
��![]() ��
��
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]()
��1����![]() �ĵ������䣻
�ĵ������䣻
��2������![]() ���ڼ���ֱ��������
���ڼ���ֱ��������![]() ���У���˵�����ɣ�
���У���˵�����ɣ�
��3����![]() ������
������![]() ���������ʵ��
���������ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������A��BCD�У���E��BD�ϣ�EA��EB��EC��ED��BD![]() CD����ACDΪ�������Σ���M��N�ֱ���AE��CD���˶��������˵㣩����AM��CN����������C��EMN�����ȡ�����ֵ
CD����ACDΪ�������Σ���M��N�ֱ���AE��CD���˶��������˵㣩����AM��CN����������C��EMN�����ȡ�����ֵ![]() ʱ������A��BCD�������ı����Ϊ_____.
ʱ������A��BCD�������ı����Ϊ_____.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
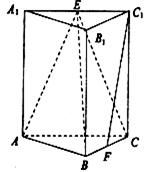
����Ŀ����ͼ��������![]() �У����ⴹֱ�ڵ��棬
�У����ⴹֱ�ڵ��棬 ![]() �ֱ���
�ֱ���![]() ���е㣮
���е㣮
��1����֤: ƽ��![]() ƽ��
ƽ��![]() ��
��
��2����֤: ![]() ƽ��
ƽ��![]() ��
��
��3��������![]() �����
�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() ����������
����������![]() ������ֱ�Ϊ
������ֱ�Ϊ![]() ��
��![]() ����
����![]() ����ֱ�ߵ�б��֮������
����ֱ�ߵ�б��֮������![]() ���Ƕ���
���Ƕ���![]() �Ĺ켣Ϊ
�Ĺ켣Ϊ![]() .
.
������![]() �Ĺ켣
�Ĺ켣![]() �ķ��̣�
�ķ��̣�
������ֱ��![]() ������
������![]() ����
����![]() ���㣬��
���㣬��![]() ������
������![]() �ϣ���
�ϣ���![]() Ϊ
Ϊ![]() �����ģ�
�����ģ�![]() Ϊ����ԭ�㣩����֤��
Ϊ����ԭ�㣩����֤��![]() �����Ϊ��ֵ��������ö�ֵ.
�����Ϊ��ֵ��������ö�ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������״��������![]() ���鷢�����������������������.��ȫ������Ĺ�ͬŬ���������ŵ��ϸ�ܿ��£��ҹ��������Ѿ��õ��˺ܺõĿ���.Ȼ����С��ͬѧ���֣�ÿ�����������鷢���ij��ڣ�������ʶ����ʹ�ʩ����λ����Ⱦ����������ֿ��ٵ�����.�±���С��ͬѧ��¼��ij������8��ÿ������״������Ⱦȷ����ۼ�����.
���鷢�����������������������.��ȫ������Ĺ�ͬŬ���������ŵ��ϸ�ܿ��£��ҹ��������Ѿ��õ��˺ܺõĿ���.Ȼ����С��ͬѧ���֣�ÿ�����������鷢���ij��ڣ�������ʶ����ʹ�ʩ����λ����Ⱦ����������ֿ��ٵ�����.�±���С��ͬѧ��¼��ij������8��ÿ������״������Ⱦȷ����ۼ�����.
���ڴ��� | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
�ۼ�ȷ������ | 4 | 8 | 16 | 31 | 51 | 71 | 97 | 122 |
Ϊ�˷����ù��ۼƸ�Ⱦ�����ı仯���ƣ�С��ͬѧ�ֱ�������ģ�ͣ���![]() ����
����![]() �Ա���
�Ա���![]() ��
��![]() �Ĺ�ϵ������ϣ��õ���Ӧ�Ļع鷽�̲����вв�������в�ͼ���£�ע���в�
�Ĺ�ϵ������ϣ��õ���Ӧ�Ļع鷽�̲����вв�������в�ͼ���£�ע���в�![]() �������������
�������������![]() ��
��![]() ��
��![]() ��
��![]() ������
������![]() ��
��![]() .
.
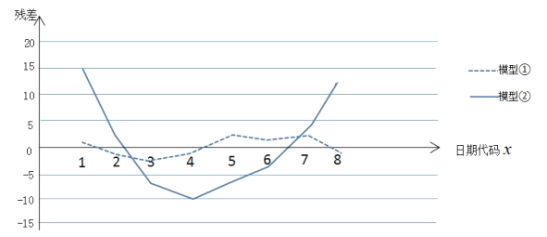
��1�����ݲв�ͼ���Ƚ�ģ�͢٣��ڵ����Ч����Ӧ��ѡ���ĸ�ģ�ͣ�����Ҫ˵�����ɣ�
��2�����ݣ�1����ѡ����ģ�������Ӧ�Ļع鷽�̣�ϵ��������һλС������
��3������ʱ��ù���ֹ��9������״������Ⱦȷ����ۼ�������δ����.С��ͬѧ��Ϊ�������������û�еõ����Ը��ƣ������ݹ���֮ǰ���Ը������ڣ�2��������Ļع鷽�����Ը�Ⱦ��������Ԥ�⣬��ô���Ƹõ�����9������״������Ⱦȷ����ۼ������Ƕ���.
�����ع�ֱ�ߵ�б�ʺͽؾ����С���˹��ƹ�ʽ�ֱ�Ϊ��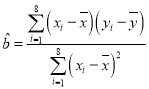 ��
��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�Է�Ϊ�˸����ǵĶ�������֧�������ϴ�ѧ�ķ��ã��Ӻ���һ�������տ�ʼ��ÿ�굽���д���![]() Ԫһ�궨�ڣ���������Ϊ
Ԫһ�궨�ڣ���������Ϊ![]() ���ֲ��䣬��ÿ�굽��ʱ������Ϣ���Զ�תΪ�µ�һ�궨�ڣ�������18������ʱ���ٴ��룬�����д�����Ϣ��ȫ��ȡ�أ���ȡ�ص�Ǯ������Ϊ
���ֲ��䣬��ÿ�굽��ʱ������Ϣ���Զ�תΪ�µ�һ�궨�ڣ�������18������ʱ���ٴ��룬�����д�����Ϣ��ȫ��ȡ�أ���ȡ�ص�Ǯ������Ϊ![]() ����
����![]()
A.![]() B.
B.![]()
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
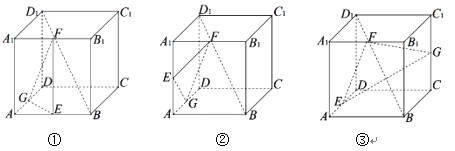
����Ŀ����ͼ������������������![]() �У�
�У�![]() ��Ϊ��������е㣬��
��Ϊ��������е㣬��![]() ��������Ľ��森�ڸ��������У�ֱ��
��������Ľ��森�ڸ��������У�ֱ��![]() ��ƽ��
��ƽ��![]() ��λ�ù�ϵ������ȷ����
��λ�ù�ϵ������ȷ����
A. ![]() ƽ��
ƽ��![]() ������ֻ�Т٣�
������ֻ�Т٣�![]() ƽ��
ƽ��![]() ������ֻ�Тڢ�
������ֻ�Тڢ�
B. ![]() ƽ��
ƽ��![]() ������ֻ�Тڣ�
������ֻ�Тڣ�![]() ƽ��
ƽ��![]() ������ֻ�Т�
������ֻ�Т�
C. .![]() ƽ��
ƽ��![]() ������ֻ�Т٣�
������ֻ�Т٣�![]() ƽ��
ƽ��![]() ������ֻ�Т�
������ֻ�Т�
D. ![]() ƽ��
ƽ��![]() ������ֻ�Тڣ�
������ֻ�Тڣ�![]() ƽ��
ƽ��![]() ������ֻ�Т�
������ֻ�Т�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com