
| A. | $3\overrightarrow i+2\overrightarrow j$ | B. | $-2\overrightarrow i+3\overrightarrow j$ | C. | $-3\overrightarrow i+2\overrightarrow j$ | D. | $2\overrightarrow i-3\overrightarrow j$ |
分析 根据题意,计算可得$2\overrightarrow i+3\overrightarrow j$=(2,3),进而依次分析选项,计算判定选项中向量与$2\overrightarrow i+3\overrightarrow j$的数量积是否为0,即可得判定向量是否垂直,综合可得答案.
解答 解:根据题意,$\overrightarrow i=(1,0)、\overrightarrow j=(0,1)$,则$2\overrightarrow i+3\overrightarrow j$=(2,3);
依次分析选项:
对于A、3$\overrightarrow{i}$+2$\overrightarrow{j}$=(3,2),($2\overrightarrow i+3\overrightarrow j$)•(3$\overrightarrow{i}$+2$\overrightarrow{j}$)=3×2+2×3=12≠0,则3$\overrightarrow{i}$+2$\overrightarrow{j}$与$2\overrightarrow i+3\overrightarrow j$不垂直;不符合题意;
对于B、-2$\overrightarrow{i}$+3$\overrightarrow{j}$=(-2,3),($2\overrightarrow i+3\overrightarrow j$)•(3$\overrightarrow{i}$+2$\overrightarrow{j}$)=2×(-2)+3×3≠0,则-2$\overrightarrow{i}$+3$\overrightarrow{j}$与$2\overrightarrow i+3\overrightarrow j$不垂直;不符合题意;
对于C、3$\overrightarrow{i}$+2$\overrightarrow{j}$=(-3,2),(3$\overrightarrow{i}$+2$\overrightarrow{j}$)•(3$\overrightarrow{i}$+2$\overrightarrow{j}$)=3×(-2)+2×3=0,则3$\overrightarrow{i}$+2$\overrightarrow{j}$与$2\overrightarrow i+3\overrightarrow j$垂直,符合题意;
对于D、2$\overrightarrow{i}$-3$\overrightarrow{j}$=(2,-3),(2$\overrightarrow{i}$-3$\overrightarrow{j}$)•(3$\overrightarrow{i}$+2$\overrightarrow{j}$)=2×2+3×(-3)≠0,则2$\overrightarrow{i}$-3$\overrightarrow{j}$与与$2\overrightarrow i+3\overrightarrow j$不垂直,不符合题意;
故选:C.
点评 本题考查平面向量的垂直的判定,涉及向量数量积的坐标运算,关键是掌握数量积的坐标计算公式.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 76 | B. | 96 | C. | 146 | D. | 188 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 编号 | 1 | 2 | 3 | 4 | 5 |
| x | 169 | 178 | 166 | 175 | 180 |
| y | 75 | 80 | 77 | 70 | 81 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
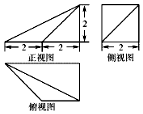
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com