
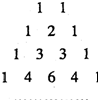 如图,“杨辉三角”中从上往下数共有n(n>7,n∈N)行,设其第k(k≤n,k∈N*)行中不是1的数字之和为ak,由a1,a2,a3,…组成的数列{an}的前n项和是Sn现有下面四个结论:①a8=254;②an=an-1+2n;③S3=22;④Sn=2n+1-2-2n.其中正确结论的序号为
如图,“杨辉三角”中从上往下数共有n(n>7,n∈N)行,设其第k(k≤n,k∈N*)行中不是1的数字之和为ak,由a1,a2,a3,…组成的数列{an}的前n项和是Sn现有下面四个结论:①a8=254;②an=an-1+2n;③S3=22;④Sn=2n+1-2-2n.其中正确结论的序号为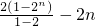 =2n+1-2n-2,故④正确
=2n+1-2n-2,故④正确

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
 如图,在杨辉三角中(三角形两腰数字为1,其余各项等于两肩数字之和),从上往下共有n行,则这些数中不是1的数字之和为( )
如图,在杨辉三角中(三角形两腰数字为1,其余各项等于两肩数字之和),从上往下共有n行,则这些数中不是1的数字之和为( )| A、2n-2n | B、2n-2n+1 | C、2n-1 | D、n2-2n+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 杨辉是我国南宋著名的数学家,“杨辉三角”是杨辉的一大重要研究成果,其中蕴含了许多优美的规律(如图),“杨辉三角”中第14行从左到右第10与第11个数的比值为
杨辉是我国南宋著名的数学家,“杨辉三角”是杨辉的一大重要研究成果,其中蕴含了许多优美的规律(如图),“杨辉三角”中第14行从左到右第10与第11个数的比值为查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在杨辉三角中,斜线l的上方从1按箭头方向可以构成一个“锯齿形”的数列{an}:1,3,3,4,6,5,10,…,记其前n项和为Sn,则S21的值为
如图,在杨辉三角中,斜线l的上方从1按箭头方向可以构成一个“锯齿形”的数列{an}:1,3,3,4,6,5,10,…,记其前n项和为Sn,则S21的值为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com