
(Ⅰ)已知y=f(x)为定义域上的增函数,且y=f(x)与y=f-1(x)的图像有公共点,求证:y=f(x)与y=f-1(x)的图像的公共点在直线y=x上;
(Ⅱ)设f(x)=ax(a>1),试讨论f(x)与f-1(x)的图像的公共点的个数.
解:(Ⅰ)设M(x0,y0)为y=f(x)与y=f-1(x)的图像的公共点则y0=f(x0) (1) y0=f-1(x0) (2)
由(2)有x0=f(y0) (3)
若x0<y0,则由(1),(3)式有:f(y0)<f(x0)又因为y=f(x)为增函数,则由f(y0)<f(x0)有:y0<x0,这与x0<y0矛盾
这说明x0<y0不可能成立,同理可证y0<x0也不可能成立所以x0=y0,即点M(x0,y0)在直线y=x上,也就是y=f(x)与y=f-1(x)的图像的公共点在直线y=x上
(Ⅱ)由(Ⅰ)知:当y=f(x)为增函数时,若y=f(x)与y=f-1(x)的图像有公共点,则这些公共点也即y=f(x)与y=x的公共点
以下讨论y=ax与y=x的公共点的个数:考虑函数g(x)=f(x)-x,即g(x)=ax-x(a>1)g′(x)=ax·lna-1,令ax·lna-1≥0有ax≥![]() =logae,即x≥loga(logae)由此知当x∈(loga(logae),+∞)时,g′(x)>0当x∈(-∞,loga(logae))时,g′(x)<0所以g(x)min=g(loga(logae))=aloga(logae)-loga(logae)=logae-loga(logae)
=logae,即x≥loga(logae)由此知当x∈(loga(logae),+∞)时,g′(x)>0当x∈(-∞,loga(logae))时,g′(x)<0所以g(x)min=g(loga(logae))=aloga(logae)-loga(logae)=logae-loga(logae)
①当logae-loga(logae)>0即lna>![]() 也就是a>
也就是a>![]() 时,g(x)min>0
时,g(x)min>0
所以f(x)=ax与y=x的图像没有公共点,因而f(x)与f-1(x)的图像没有公共点
②当logae-loga(logae)=0即a=![]() 时,f(x)与f-1(x)的图像有唯一公共点
时,f(x)与f-1(x)的图像有唯一公共点
③当logae-loga(logae)<0即1<0<![]() 时,f(x)与f-1(x)的图像有两个公共点
时,f(x)与f-1(x)的图像有两个公共点


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| 3 | x |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1-x | 4x |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1-x | 4x |
查看答案和解析>>
科目:高中数学 来源:同步题 题型:解答题
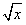 ;
; 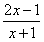 。
。 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com