
【题目】已知函数![]() ,其中常数
,其中常数![]() .
.
(1)当![]() 时,
时,![]() 的最小值;
的最小值;
(2)讨论函数的奇偶性,并说明理由;
(3)当![]() 时,是否存在实数
时,是否存在实数![]() ,使得不等式
,使得不等式![]() 对任意
对任意![]() 恒成立?若存在,求出所有满足条件的
恒成立?若存在,求出所有满足条件的![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:
【题目】某公司生产的某批产品的销售量![]() 万件(生产量与销售量相等)与促销费用
万件(生产量与销售量相等)与促销费用![]() 万元满足
万元满足![]() (其中
(其中![]() ,
,![]() 为正常数).已知生产该产品还需投入成本
为正常数).已知生产该产品还需投入成本![]() 万元(不含促销费用),产品的销售价格定为
万元(不含促销费用),产品的销售价格定为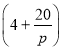 元
元![]() 件.
件.
(1)将该产品的利润![]() 万元表示为促销费用
万元表示为促销费用![]() 万元的函数;
万元的函数;
(2)促销费用投入多少万元时,该公司的利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂因排污比较严重,决定着手整治,一个月时污染度为![]() ,整治后前四个月的污染度如下表:
,整治后前四个月的污染度如下表:
月数 |
|
|
|
| … |
污染度 |
|
|
|
| … |
污染度为![]() 后,该工厂即停止整治,污染度又开始上升,现用下列三个函数模拟从整治后第一个月开始工厂的污染模式:
后,该工厂即停止整治,污染度又开始上升,现用下列三个函数模拟从整治后第一个月开始工厂的污染模式:![]() ,
,![]() ,
,![]() ,其中
,其中![]() 表示月数,
表示月数,![]() 、
、![]() 、
、![]() 分别表示污染度.
分别表示污染度.
(1)问选用哪个函数模拟比较合理,并说明理由;
(2)若以比较合理的模拟函数预测,整治后有多少个月的污染度不超过![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列![]() 各项均不为0,前n项和为
各项均不为0,前n项和为![]() ,
,![]() ,
,![]() 的前n项和为
的前n项和为![]() ,且
,且![]()
(1)若数列![]() 共3项,求所有满足要求的数列;
共3项,求所有满足要求的数列;
(2)求证:![]() 是满足已知条件的一个数列;
是满足已知条件的一个数列;
(3)请构造出一个满足已知条件的无穷数列![]() ,并使得
,并使得![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A是以BC为直径的圆O上异于B,C的动点,P为平面ABC外一点,且平面PBC⊥平面ABC,BC=3,PB=2![]() ,PC
,PC![]() ,则三棱锥P﹣ABC外接球的表面积为______.
,则三棱锥P﹣ABC外接球的表面积为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在坐标原点,且经过点
的中心在坐标原点,且经过点![]() ,它的一个焦点与抛物线
,它的一个焦点与抛物线![]() 的焦点重合.
的焦点重合.
(1)求椭圆![]() 的方程;
的方程;
(2)斜率为![]() 的直线过点
的直线过点![]() ,且与抛物线
,且与抛物线![]() 交于
交于![]() 两点,设点
两点,设点![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 的值;
的值;
(3)若直线![]() 过点
过点![]()
![]() ,且与椭圆
,且与椭圆![]() 交于
交于![]() 两点,点
两点,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,直线
,直线![]() 的纵截距为
的纵截距为![]() ,证明:
,证明:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题是真命题的是( )
A.有两个面相互平行,其余各面都是平行四边形的多面体是棱柱
B.正四面体是四棱锥
C.有一个面是多边形,其余各面都是三角形的多面体叫做棱锥
D.正四棱柱是平行六面体
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】李克强总理在很多重大场合都提出“大众创业,万众创新”.某创客,白手起家,2015年一月初向银行贷款十万元做创业资金,每月获得的利润是该月初投入资金的![]() .每月月底需要交纳房租和所得税共为该月全部金额(包括本金和利润)的
.每月月底需要交纳房租和所得税共为该月全部金额(包括本金和利润)的![]() ,每月的生活费等开支为3000元,余款全部投入创业再经营.如此每月循环继续.
,每月的生活费等开支为3000元,余款全部投入创业再经营.如此每月循环继续.
(1)问到2015年年底(按照12个月计算),该创客有余款多少元?(结果保留至整数元)
(2)如果银行贷款的年利率为![]() ,问该创客一年(12个月)能否还清银行贷款?
,问该创客一年(12个月)能否还清银行贷款?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】按照如下规则构造数表:第一行是:2;第二行是:![]() ;即3,5,第三行是:
;即3,5,第三行是:![]() 即4,6,6,8;
即4,6,6,8;![]() (即从第二行起将上一行的数的每一项各项加1写出,再各项加3写出)
(即从第二行起将上一行的数的每一项各项加1写出,再各项加3写出)
2
3,5
4,6,6,8
5,7,7,9,7,9,9,11
……………………………………
若第![]() 行所有的项的和为
行所有的项的和为![]() .
.
(1)求![]() ;
;
(2)试求![]() 与
与![]() 的递推关系,并据此求出数列
的递推关系,并据此求出数列![]() 的通项公式;
的通项公式;
(3)设![]() ,求
,求![]() 和
和![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com