
分析 (1)通过$\overrightarrow{P{F_1}}+\overrightarrow{P{F_2}}=2\overrightarrow{PO}$(O为坐标原点),推出$|\overrightarrow{PO}{|_{min}}=1$,即可求$|\overrightarrow{P{F_1}}+\overrightarrow{P{F_2}}|$的最小值.
(2)利用OP⊥OQ.推出线段PQ中点的横坐标为$\frac{1}{2}$.设直线PQ的方程为y=kx+b,联立直线与椭圆方程组,设P(x1,y1),Q(x2,y2),利用韦达定理,推出1+2k2=-4kb,①通过x1x2+y1y2=0,求出 4k2b2+2k3b-2k2+3b2+kb-2=0,②,然后求解即可.
解答 (本题满分15分)
解:(1)因为$\overrightarrow{P{F_1}}+\overrightarrow{P{F_2}}=2\overrightarrow{PO}$(O为坐标原点),
显然$|\overrightarrow{PO}{|_{min}}=1$,
所以$|\overrightarrow{P{F_1}}+\overrightarrow{P{F_2}}|$的最小值为2. …(5分)
(2)由题意,可知OP⊥OQ.
又F2P⊥F2Q,所以PQ是两个直角三角形POQ和PF2Q的公共斜边,即得线段PQ的中点到O,F2两点的距离相等,即线段PQ中点的横坐标为$\frac{1}{2}$.
设直线PQ的方程为y=kx+b,联立椭圆方程,得
(1+2k2)x2+4kbx+2b2-2=0.
设P(x1,y1),Q(x2,y2),则x1+x2=-$\frac{4kb}{{1+2{k^2}}}$.
又因为 x1+x2=1,
所以 1+2k2=-4kb,①
另一方面,x1x2=$\frac{{2{b^2}-2}}{{1+2{k^2}}}$,y1y2=$\frac{{2{k^2}{b^2}-2{k^2}}}{{1+2{k^2}}}+kb+{b^2}$.
由x1x2+y1y2=0,得$\frac{{2{b^2}-2}}{{1+2{k^2}}}+\frac{{2{k^2}{b^2}-2{k^2}}}{{1+2{k^2}}}+kb+{b^2}=0$,
即 4k2b2+2k3b-2k2+3b2+kb-2=0,②
由①②,得-20k4-20k2+3=0,解之得${k^2}=\frac{{-5+2\sqrt{10}}}{10}$.…(15分)
点评 本题考查直线与椭圆位置关系的综合应用,向量在几何中的应用,考查转化思想以及计算能力.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
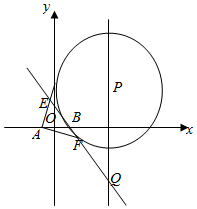 如图,P是直线x=4上一动点,以P为圆心的圆Γ经定点B(1,0),直线l是圆Γ在点B处的切线,过A(-1,0)作圆Γ的两条切线分别与l交于E,F两点.
如图,P是直线x=4上一动点,以P为圆心的圆Γ经定点B(1,0),直线l是圆Γ在点B处的切线,过A(-1,0)作圆Γ的两条切线分别与l交于E,F两点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | (1.75,2) | C. | (1.5,2) | D. | (1,1.5) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
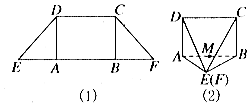 如图所示,在等腰梯形CDEF中,DE=CD=$\sqrt{2}$,EF=2+$\sqrt{2}$,将它沿着两条高AD,CB折叠成如图(2)所示的四棱锥E-ABCD(E,F重合).
如图所示,在等腰梯形CDEF中,DE=CD=$\sqrt{2}$,EF=2+$\sqrt{2}$,将它沿着两条高AD,CB折叠成如图(2)所示的四棱锥E-ABCD(E,F重合).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x<-1或x>1} | B. | {x|2<x<3} | C. | {x|-1<x<3} | D. | {x|x<-1或x>3} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com