
【题目】(本小题满分12分)
已知![]() =12sin(x+
=12sin(x+![]() )cosx-3,x∈[o,
)cosx-3,x∈[o,![]() ].
].
(1)求![]() 的最大值、最小值;
的最大值、最小值;
(Ⅱ)CD为△ABC的内角平分线,已知AC=![]() max,BC=
max,BC=![]() ,CD=2
,CD=2![]() ,求∠C.
,求∠C.
【答案】( Ⅰ) ![]() max =6 ,
max =6 , ![]() min =3.
min =3.
( Ⅱ ) C=![]() .
.
【解析】分析:第一问先对函数解析式进行化简,首先应用正弦的和角公式拆,之后应用正余弦的倍角公式降次升角,之后应用辅助角公式化简,之后将整体角的取值范围求出,再判断其最值,第二问先将第一问求的结果代入,之后借助于正余弦定理找出对应的量,求得结果.
详解:( Ⅰ )![]() =6sin ( 2 x +
=6sin ( 2 x + ![]() )
)
∵ ![]() 在( 0 ,
在( 0 ,![]() )上单调递增,(
)上单调递增,(![]() )上单调递减
)上单调递减
∴ ![]() max =6 ,
max =6 , ![]() min =3
min =3
( Ⅱ )在 ΔADC 中,![]() =
=![]() ,在 ΔBDC中,
,在 ΔBDC中,![]() =
=![]()
∵sin∠ADC=sin∠ BDC , AC=6 , BC =3
∴ AD=2BD 在ΔBCD中, BD2 =17-12![]() cos
cos![]() ,
,
在ΔACD中, AD2=44-24![]() cos
cos![]() =68-48
=68-48![]() cos
cos![]()
∴cos![]() =
=![]() ,即 C=( Ⅰ)
,即 C=( Ⅰ) ![]() max =6 ,
max =6 , ![]() min =3.
min =3.
( Ⅱ ) C=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数)。曲线
为参数)。曲线![]() 的参数方程为
的参数方程为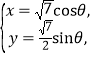 (
(![]() 为参数),在以坐标原点为极点,
为参数),在以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)求曲线![]() ,
,![]() 的极坐标方程;
的极坐标方程;
(2)在极坐标系中,射线![]() 与曲线
与曲线![]() 交于点
交于点![]() ,射线
,射线![]() 与曲线
与曲线![]() 交于点
交于点![]() ,求
,求![]() 的面积(其中
的面积(其中![]() 为坐标原点).
为坐标原点).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|y=lg(x-![]() )},B={x|
)},B={x|![]() -cx<0,c>0},若AB,则实数c的取值范围是( )
-cx<0,c>0},若AB,则实数c的取值范围是( )
A.(0,1]B.[1,+∞)
C.(0,1)D.(1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校100名学生的数学测试成绩的频率分布直方图如图所示,分数不低于a即为优秀,如果优秀的人数为20,则a的估计值是( )
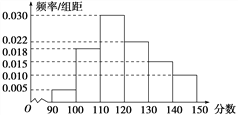
A. 130 B. 140 C. 133 D. 137
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机抽取了40辆汽车在经过路段上某点时的车速(km/h),现将其分成六段: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,后得到如图所示的频率分布直方图.
,后得到如图所示的频率分布直方图.
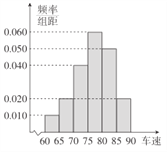
(Ⅰ)现有某汽车途经该点,则其速度低于80km/h的概率约是多少?
(Ⅱ)根据直方图可知,抽取的40辆汽车经过该点的平均速度约是多少?
(Ⅲ)在抽取的40辆且速度在![]() (km/h)内的汽车中任取2辆,求这2辆车车速都在
(km/h)内的汽车中任取2辆,求这2辆车车速都在![]() (km/h)内的概率.
(km/h)内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB是圆O的直径,点C是圆O上异于A,B的点,PO垂直于圆O所在的平面,且PO=OB=1.
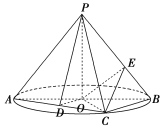
(1)若D为线段AC的中点,求证:AC⊥平面PDO;
(2)求三棱锥P-ABC体积的最大值;
(3)若![]() ,点E在线段PB上,求CE+OE的最小值.
,点E在线段PB上,求CE+OE的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com