
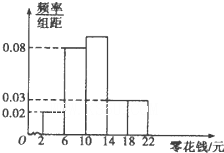
 一所中学共有4000名学生,为了引导学生树立正确的消费观,需抽样调查学生每天使用零花钱的数量(取整数元)情况,分层抽取容量为300的样本,作出频率分布直方图如图所示,请估计在全校所有学生中,一天使用零花钱在6元~14元的学生大约有
一所中学共有4000名学生,为了引导学生树立正确的消费观,需抽样调查学生每天使用零花钱的数量(取整数元)情况,分层抽取容量为300的样本,作出频率分布直方图如图所示,请估计在全校所有学生中,一天使用零花钱在6元~14元的学生大约有 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:高中数学 来源: 题型:
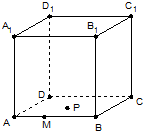 如图,正方体ABCD-A1B1C1D1的棱长为1,点M在棱AB上,且PB,点AM=
如图,正方体ABCD-A1B1C1D1的棱长为1,点M在棱AB上,且PB,点AM=| 1 |
| 3 |
| A、圆 | B、抛物线 | C、双曲线 | D、椭圆 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、直线m在平面β内 |
| B、直线m与平面β相交但不垂直 |
| C、直线m与平面β垂直 |
| D、直线m与平面β平行 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、“f(O)=O”是“函数f(x)是奇函数”的充要条件 | ||||||||
| B、“向量a,b,c,若a•b=a•c,则b=c”是真命题 | ||||||||
C、函数f(x)=
| ||||||||
D、“若α=
|
查看答案和解析>>
科目:高中数学 来源: 题型:
A、?x∈R,sinx+
| ||
B、?x∈R,
| ||
| C、命题p:“?x∈R,x2-x-1>0”的否定¬p:“?x∈R,x2-x-1≤0” | ||
| D、“ea>eb”是“log2a>log2b”的充要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com