
【题目】对于由2n个质数组成的集合![]() ,可将其元素两两搭配成n个乘积,得到一个n元集.若
,可将其元素两两搭配成n个乘积,得到一个n元集.若![]() 与
与![]() 是由此得到的两个n元集,其中,
是由此得到的两个n元集,其中, ![]() ,且
,且![]() ,则称集合对{A ,B}是由M炮制成的一幅“对联”(如由四元集{a,b,c,d}可炮制成三幅对联:
,则称集合对{A ,B}是由M炮制成的一幅“对联”(如由四元集{a,b,c,d}可炮制成三幅对联:
![]()
![]() .
.
求六元质数集M={a,b,c,d,e,f}所能炮制成的对联数.
【答案】60
【解析】
六个元素可以形成十五个不同的“字条”,列出如下:![]()
![]() ,
,![]() ,
,
![]() .
.
将位于第i行、第j列交叉处的字条看作一个坐标点,记为(i,j).
对于第一行的(1,1),它与下面每行各有两个搭配:![]() ;
;![]() ;
;
![]() .共得4×2=8个搭配.
.共得4×2=8个搭配.
类似地,点(1,2)及(1,3)与下面四行的点也各有8个搭配.
于是,第一行的三个点与下面四行的点共形成3×4×2=24个搭配;
第二行的每个点与下面每行的点也各有两个搭配,共得3×3×2=18个搭配;
第三行的每个点与下面每行的点也各有两个搭配,共得3×2×2=12个搭配;
第四行的每个点与下行的点也各有两个搭配,共得3×1×2=6个搭配.
故搭配数为6×(1+2+3+4)=60个,即由集M可炮制出60幅对联.


科目:高中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣(2m+3)x+m2+2=0.
(1)若方程有实数根,求实数m的取值范围;
(2)若方程两实数根分别为x1、x2,且满足x12+x22=31+|x1x2|,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(2ωx+![]() )+sin(2ωx-
)+sin(2ωx-![]() )+2cos2ωx,其中ω>0,且函数f(x)的最小正周期为π
)+2cos2ωx,其中ω>0,且函数f(x)的最小正周期为π
(1)求ω的值;
(2)求f(x)的单调增区间
(3)若函数g(x)=f(x)-a在区间[-![]() ,
,![]() ]上有两个零点,求实数a的取值范围.
]上有两个零点,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知点![]() 是曲线
是曲线![]() 上的动点,求点
上的动点,求点![]() 到曲线
到曲线![]() 的最小距离.
的最小距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高中生在被问及“家,朋友聚集的地方,个人空间”三个场所中“感到最幸福的场所在哪里?”这个问题时,从中国某城市的高中生中,随机抽取了55人,从美国某城市的高中生中随机抽取了45人进行答题.中国高中生答题情况是:选择家的占![]() 、朋友聚集的地方占
、朋友聚集的地方占![]() 、个人空间占
、个人空间占![]() .美国高中生答题情况是:朋友聚集的地方占
.美国高中生答题情况是:朋友聚集的地方占![]() 、家占
、家占![]() 、个人空间占
、个人空间占![]() .如下表:
.如下表:
在家里最幸福 | 在其它场所幸福 | 合计 | |
中国高中生 | |||
美国高中生 | |||
合计 |
(Ⅰ)请将![]() 列联表补充完整;试判断能否有
列联表补充完整;试判断能否有![]() 的把握认为“恋家”与否与国别有关;
的把握认为“恋家”与否与国别有关;
(Ⅱ)从被调查的不“恋家”的美国学生中,用分层抽样的方法选出4人接受进一步调查,再从4人中随机抽取2人到中国交流学习,求2人中含有在“个人空间”感到幸福的学生的概率.
附:![]() ,其中
,其中![]() .
.
| 0.050 | 0.025 | 0.010 | 0.001 |
| 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某医疗器械公司在全国共有![]() 个销售点,总公司每年会根据每个销售点的年销量进行评价分析.规定每个销售点的年销售任务为一万四千台器械.根据这
个销售点,总公司每年会根据每个销售点的年销量进行评价分析.规定每个销售点的年销售任务为一万四千台器械.根据这![]() 个销售点的年销量绘制出如下的频率分布直方图.
个销售点的年销量绘制出如下的频率分布直方图.
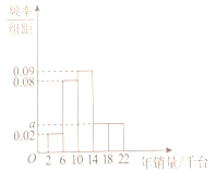
(1)完成年销售任务的销售点有多少个?
(2)若用分层抽样的方法从这![]() 个销售点中抽取容量为
个销售点中抽取容量为![]() 的样本,求该五组
的样本,求该五组![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,(单位:千台)中每组分别应抽取的销售点数量.
,(单位:千台)中每组分别应抽取的销售点数量.
(3)在(2)的条件下,从前两组![]() ,
,![]() 中的销售点随机选取
中的销售点随机选取![]() 个,记这
个,记这![]() 个销售点在
个销售点在![]() 中的个数为
中的个数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com