
(08年重庆卷文)(本小题满分12分,(Ⅰ)小问6分,(Ⅱ)小问6分.)
如图(20)图, ![]() 为平面,
为平面,![]() AB=5,A,B在棱l上的射影分别为A′,B′,AA′=3,BB′=2.若二面角
AB=5,A,B在棱l上的射影分别为A′,B′,AA′=3,BB′=2.若二面角![]() 的大小为
的大小为![]() ,求:
,求:
(Ⅰ)点B到平面![]() 的距离;
的距离;
(Ⅱ)异面直线l与AB所成的角(用反三角函数表示).

解:(1)如答(20)图,
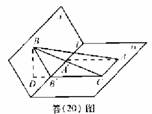
过点B′C∥A′A且使B′C=A′A.过点B作BD⊥CB′,交CB′的延长线于D.
由已知AA′⊥l,可得DB′⊥l,又已知BB′⊥l,故l⊥平面BB′D,得BD⊥l又因BD⊥CB′,从而BD⊥平面α,BD之长即为点B到平面α的距离.
因B′C⊥l且BB′⊥l,故∠BB′C为二面角α-l-β的平面角.由题意,∠BB′C=
![]() .因此在Rt△BB′D中,BB′=2,∠BB′D=π-∠BB′C=
.因此在Rt△BB′D中,BB′=2,∠BB′D=π-∠BB′C=![]() ,BD=BB′?sinBB′D
,BD=BB′?sinBB′D
=![]() .
.
(Ⅱ)连接AC、BC.因B′C∥A′A,B′C=A′A,AA′⊥l,知A′ACB′为矩形,故AC∥l.所以∠BAC或其补角为异面直线l与AB所成的角.
在△BB′C中,B′B=2,B′C=3,∠BB′C=![]() ,则由余弦定理,
,则由余弦定理,
BC=![]() .
.
因BD![]() 平面
平面![]()
![]() ,且DC
,且DC![]() CA,由三垂线定理知AC
CA,由三垂线定理知AC![]() BC.
BC.
故在△ABC中,∠BCA=![]()
![]() ,sinBAC=
,sinBAC=![]() .
.
因此,异面直线l与AB所成的角为arcsin![]()


科目:高中数学 来源: 题型:
(08年重庆卷文)某交高三年级有男生500人,女生400人,为了解该年级学生的健康情况,从男生中任意抽取25人,从女生中任意抽取20人进行调查.这种抽样方法是
(A)简单随机抽样法 (B)抽签法 (C)随机数表法 (D)分层抽样法
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年重庆卷文)曲线C:![]() (
(![]() 为参数)的普通方程为
为参数)的普通方程为
(A)(x-1)2+(y+1)2=1 (B) (x+1)2+(y+1)2=1 (C) (x-1)2+(y-1)2=1 (D) (x-1)2+(y-1)2=1
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年重庆卷文)设x是实数,则“x>0”是“|x|>0”的
(A)充分而不必要条件 (B)必要而不充分条件
(C)充要条件 (D)既不充分也不必要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com