
【题目】如图是某市3月1日至14日的空气质量指数趋势图.空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染.某人随机选择3月1日至3月13日中的某一天到达该市,并停留2天.
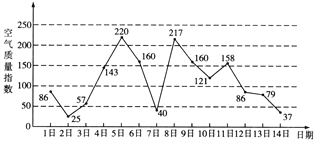
(Ⅰ)求3月1日到14日空气质量指数的中位数;
(Ⅱ)求此人到达当日空气重度污染的概率;
(Ⅲ)由图判断从哪天开始连续三天的空气质量指数方差最大?(结论不要求证明)
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以直角坐标系的原点
为参数).以直角坐标系的原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立坐标系,曲线
轴的正半轴为极轴建立坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)若过点![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,与
两点,与![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高科技企业生产产品A和产品B需要甲、乙两种新型材料.生产一件产品A需要甲材料![]() ,乙材料
,乙材料![]() .用5个工时;生产一件产品B需要甲材料
.用5个工时;生产一件产品B需要甲材料![]() ,乙材料
,乙材料![]()
![]() ,用3个工时。生产一件产品A的利润为2100元,生产一件产品B的利润为900元,该企业现有甲材料150
,用3个工时。生产一件产品A的利润为2100元,生产一件产品B的利润为900元,该企业现有甲材料150![]() ,乙材料
,乙材料![]() ,则在不超过600个工时的条件下,生产产品A,产品B的利润之和的最大值为______________元.
,则在不超过600个工时的条件下,生产产品A,产品B的利润之和的最大值为______________元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),在以坐标原点为极点,
),在以坐标原点为极点,![]() 轴非负轴为极轴的极坐标系中,曲线
轴非负轴为极轴的极坐标系中,曲线![]() :
:![]() (
(![]() 为极角).
为极角).
(1)将曲线![]() 化为极坐标方程,当
化为极坐标方程,当![]() 时,将
时,将![]() 化为直角坐标方程;
化为直角坐标方程;
(2)若曲线![]() 与
与![]() 相交于一点
相交于一点![]() ,求
,求![]() 点的直角坐标使
点的直角坐标使![]() 到定点
到定点![]() 的距离最小.
的距离最小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆M:![]() 长轴上的两个顶点为
长轴上的两个顶点为![]() 、
、![]() ,点P为椭圆M上除
,点P为椭圆M上除![]() 、
、![]() 外的一个动点,若
外的一个动点,若![]() 且
且![]() ,则动点Q在下列哪种曲线上运动( )
,则动点Q在下列哪种曲线上运动( )
A. 圆 B. 椭圆 C. 双曲线 D. 抛物线
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《汉字听写大会》不断创收视新高,为了避免“书写危机”弘扬传统文化,某市大约10万名市民进行了汉字听写测试.现从某社区居民中随机抽取50名市民的听写测试情况,发现被测试市民正确书写汉字的个数全部在![]() 到
到![]() 之间,将测试结果按如下方式分成六组:第一组
之间,将测试结果按如下方式分成六组:第一组![]() ,第二组
,第二组![]() ,…,第六组
,…,第六组![]() ,如图是按上述分组方法得到的频率分布直方图.
,如图是按上述分组方法得到的频率分布直方图.
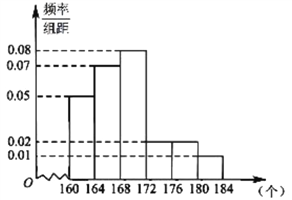
(1)若电视台记者要从抽取的市民中选1人进行采访,求被采访人恰好在第1组或第4组的概率;
(2)已知第5,6两组市民中有3名女性,组织方要从第5,6两组中随机抽取2名市民组成弘扬传统文化宣传队,求至少有1名女性市民的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的下顶点为
的下顶点为![]() ,右顶点为
,右顶点为![]() ,离心率
,离心率![]() ,抛物线
,抛物线![]() 的焦点为
的焦点为![]() ,
,![]() 是抛物线
是抛物线![]() 上一点,抛物线
上一点,抛物线![]() 在点
在点![]() 处的切线为
处的切线为![]() ,且
,且![]() .
.
(1)求直线![]() 的方程;
的方程;
(2)若![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,且
两点,且![]() ,求
,求![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com